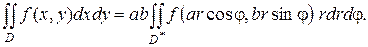Замена переменных в двойном интеграле
Пусть в двойном интеграле  прямоугольные координаты
прямоугольные координаты  преобразуются к новым координатам
преобразуются к новым координатам  которые связаны с
которые связаны с  соотношениями:
соотношениями:
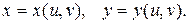 (1.10)
(1.10)
Если между областями  и
и 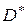 , лежащими в плоскостях
, лежащими в плоскостях  и
и  (рисунок 1.4), установлено соотношениями (1.10) взаимно однозначное отображение, причем функции (1.10) имеют непрерывные частные производные первого порядка в области
(рисунок 1.4), установлено соотношениями (1.10) взаимно однозначное отображение, причем функции (1.10) имеют непрерывные частные производные первого порядка в области 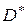 и якобиан отображения в области
и якобиан отображения в области 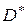 не обращается в нуль, т.е.
не обращается в нуль, т.е.

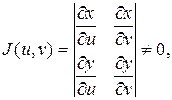
то имеет место следующая формула замены переменных в двойном интеграле:

 (1.11)
(1.11)

Рисунок 1.4
В полярных координатах формулы (1.10) имеют вид 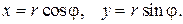 Эти формулы связывают прямоугольные координаты
Эти формулы связывают прямоугольные координаты 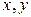 с полярными координатами
с полярными координатами  при условии, что полюс помещен в начало координат и полярная ось направлена вдоль оси
при условии, что полюс помещен в начало координат и полярная ось направлена вдоль оси 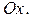 В этом случае
В этом случае 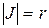 и формула (1.11) принимает вид
и формула (1.11) принимает вид 

| 
|
Рисунок 1.5 Рисунок 1.6
Для области 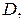 ограниченной лучами, образующими с полярной осью углы
ограниченной лучами, образующими с полярной осью углы  и
и 
 , и кривыми
, и кривыми  и
и 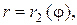 причем
причем 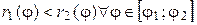 (рисунок 1.5), получаем
(рисунок 1.5), получаем
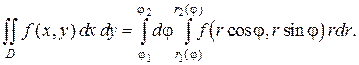 (1.12)
(1.12)
Если область D содержит начало координат (рисунок 1.6), то
 (1.13)
(1.13)
Формулы (1.12) и (1.13) удобно использовать при решении задач, когда область  есть круг или часть круга.
есть круг или часть круга.
Обобщенными полярными координатами называют переменные  и
и 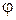 , связанные с прямоугольными координатами
, связанные с прямоугольными координатами 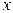 и
и 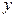 формулами
формулами  где
где 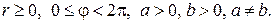 В этом случае
В этом случае  и формула (1.11) принимает вид
и формула (1.11) принимает вид