рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Военное дело
- /
- Поверхностные интегралы первого рода
Реферат Курсовая Конспект
Поверхностные интегралы первого рода
Поверхностные интегралы первого рода - раздел Военное дело, ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ Двойной интеграл Двойной интеграл и его приложения Пусть ...
Пусть  функция, непрерывная на некоторой гладкой ограниченной поверхности
функция, непрерывная на некоторой гладкой ограниченной поверхности  . Разобьем поверхность
. Разобьем поверхность  на
на  частей
частей  , не имеющих общих внутренних точек, и в каждой части
, не имеющих общих внутренних точек, и в каждой части 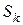 выберем произвольную точку
выберем произвольную точку  Составим интегральную сумму
Составим интегральную сумму
 (2.7)
(2.7)
где 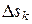 ― площадь
― площадь 
Пусть  Если интегральная сумма (2.7) имеет предел при
Если интегральная сумма (2.7) имеет предел при  не зависящий от способа дробления поверхности
не зависящий от способа дробления поверхности  на части
на части 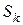 и от выбора точек
и от выбора точек 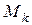 в них, то этот предел называется поверхностным интегралом 1-го рода от функции
в них, то этот предел называется поверхностным интегралом 1-го рода от функции  по поверхности
по поверхности  и обозначается
и обозначается  т.е.
т.е.
 (2.8)
(2.8)
Если через 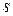 обозначить площадь поверхности
обозначить площадь поверхности  , то из формулы (2.8) следует при
, то из формулы (2.8) следует при 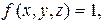 что
что
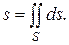 (2.9)
(2.9)
Если на поверхности  распределена с плотностью
распределена с плотностью  некоторая масса
некоторая масса  , то
, то
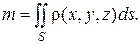 (2.10)
(2.10)
Координаты центра масс, статические моменты и моменты инерции материальной поверхности вычисляются по формулам, аналогичным формулам (1.5) ― (1.7).
Если поверхность  задана уравнением
задана уравнением 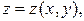 то вычисление поверхностного интеграла сводится к вычислению двойного интеграла по области
то вычисление поверхностного интеграла сводится к вычислению двойного интеграла по области  - проекции поверхности
- проекции поверхности  на плоскость
на плоскость  :
:
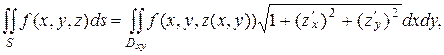 (2.11)
(2.11)
где  Формула (2.9) для вычисления площади в этом случае принимает вид
Формула (2.9) для вычисления площади в этом случае принимает вид
 (2.12)
(2.12)
Если гладкая поверхность  задана параметрическими уравнениями
задана параметрическими уравнениями


где функции 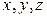 имеют непрерывные частные производные первого порядка в замкнутой области
имеют непрерывные частные производные первого порядка в замкнутой области 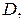 то
то
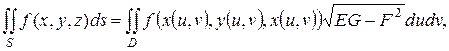 (2.13)
(2.13)
где
 (2.14)
(2.14)
– Конец работы –
Эта тема принадлежит разделу:
ДВОЙНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ Двойной интеграл Двойной интеграл и его приложения
стр... Введение Двойные и тройные интегралы Двойной интеграл...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Поверхностные интегралы первого рода
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов