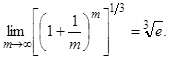Теорема 2 (второй замечательный предел)

Существует предел .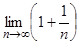

Доказательство. Рассмотрим последовательность с общим членом

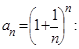
Покажем, что эта последовательность возрастающая и ограниченная. Для этого воспользуемся формулой бинома Ньютона:

.

Преобразуем по этой формуле 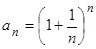, полагая :

.

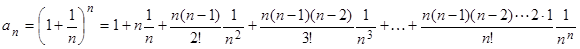В полученном выражении:

третье слагаемое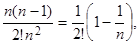

четвертое =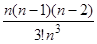

и т.д., а последнее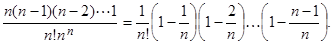

Получаем:

(*)

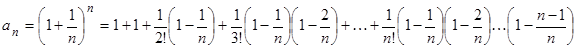Покажем, что последовательность возрастающая, т.е. :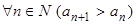

(**)

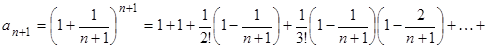
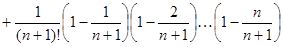Так как то 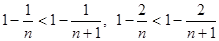и т.д., поэтому каждое слагаемое (начиная с третьего) из равенства (*) меньше соответствующего слагаемого из равенства (**), кроме того, в равенстве (**) правая часть содержит на одно (положительное) слагаемое больше. Отсюда заключаем, что .

Покажем, что последовательность ограничена (сверху), т.е.

Если в равенстве (**) каждую из скобок 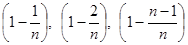заменить на 1 (на большее число), то получим неравенство:

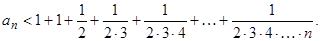
Так как 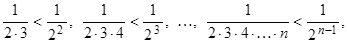то

.

По формуле суммы геометрической прогрессии имеем:

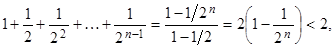поэтому .

Последовательность 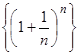возрастает и ограничена сверху, по теореме 1 существует предел, этот предел называют неперовым числом и обозначают через e. Итак,

.

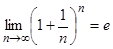Так как 2 < a_n < 3, то 2 < 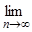a_n 3, т.е. 2 < e 3. Это число e иррациональное и e 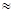2,718282.

Число e широко используется как основание для показательной функции (экспонента) и как основание для логарифмов (натуральные логарифмы).

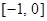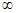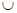Рассмотрим (рис. 1.13) функцию y = , которая не определена на отрезке (подумайте почему?). Ее область определения (–, –1)(0, +).

Известно, что

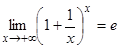и .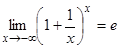

Нетрудно показать, что

.

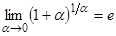Все записанные пределы объединяются одним названием второго замечательного предела.

Рассмотрим применение второго замечательногопредела для вычисления некоторых пределов.

Пример.Найти

Решение. Обозначим: 3n = m, n = 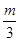. Если n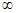, то m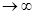и мы получим:

=
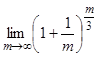