Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции

Пусть a(x) и b(x) – б.м. функции при x ® a (x® + ¥, x ® –¥, x ® x₀, ...). Рассмотрим предел их отношения при x ® a.

1. Если = b и b – конечное число, b ¹ 0, то функции a(x), b(x) называются бесконечно малыми одного порядка малости при x ® a.

2. Если = 0, то a(x) называют бесконечно малой высшего порядка, чем b(x) при x ® a. Очевидно, в этом случае = ¥.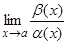

3. Если a(x) – б.м. высшего порядка, чем b(x), и = b ¹ 0 (b – конечное число, k Î N), то a(x) называют бесконечно малой k-го порядка, по сравнению с b(x) при x ® a.

4. Если не существует 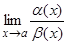(ни конечный, ни бесконечный), то a(x), b(x) называют несравнимыми б.м. при x ® a.

5. Если 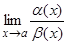= 1, то a(x), b(x) называются эквивалентными б.м. при x ® a, что обозначается так: a(x) ~ b(x) при x ® a.

Пример 1. a(x) = (1 – x)³, b (x) = 1 – x³.

Очевидно, что при x ® 1 функции a(x), b(x) являются б.м. Для их сравнения найдем предел их отношения при x ® 1:

=

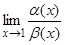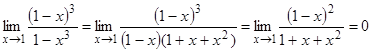
Вывод: a(x) является б.м. высшего порядка, по сравнению с b(x) при x ® 1.

Нетрудно убедиться, что = 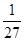(убедитесь!), откуда следует, что a(x) – б.м. 3-го порядка малости, по сравнению с b(x) при x ® 1.

Пример 2. Функции a₁(x) = 4x, a₂ (x) = x², a₃(x) = sinx, a₄(x) = tgx являются бесконечно малыми при x ® 0. Сравним их:

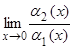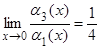= 0, , = 1, = ¥.

Отсюда заключаем, что a₂(x) = x² – б.м. высшего порядка, по сравнению с a₁(x) и a₃(x) (при x ® 0), a₁(x) и a₃(x) – б.м. одного порядка, a₃(x) и a₄(x) – эквивалентные б.м., т.е. sinx ~ tgx при x ® 0.

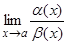Теорема 1. Пусть a(x) ~ a₁(x), b(x) ~ b₁(x) при x ® a. Если существует , то существует и , и = .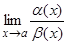

Доказательство. 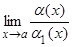= 1, = 1,

= = .

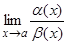Эта теорема позволяет упрощать нахождение пределов.

Пример 3. Найти .

В силу первого замечательного предела sin4x ~ 4x, tg3x ~ 3x при x ® 0, поэтому

= =.

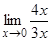Теорема 2. Бесконечно малые функции a(x) и b(x) эквивалентны (при x ® a) тогда и только тогда, когда a(x) – b(x) является б.м. высшего порядка, по сравнению с a(x) и b(x) (при x ® a).