рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Охрана труда
- /
- Множества
Реферат Курсовая Конспект
Множества
Множества - раздел Охрана труда, Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности Понятие Множества Является Первоначальным Понятием Математики, Точное Определ...
Понятие множества является первоначальным понятием математики, точное определение ему не дается, но его можно пояснить, описать через другие понятия. Можно сказать, что множество – это совокупность, собрание каких-то объектов, предметов, при этом объект, входящий в это множество, называют его элементом. Множества могут содержать как конечное число элементов, так и бесконечно много элементов. Рассматривают и множество, не содержащее элементов, его называют пустым и обозначают символом Æ.
В математическом анализе чаще всего рассматриваются числовые множества, за некоторыми из них закреплены специальные обозначения. Так, множество всех натуральных чисел обозначаются через N и записывают так: N = {1,2,3,...}. Далее, через Z обозначают множество всех целых чисел, содержащее как натуральные числа, так и 0, и целые отрицательные числа; Z= {..., –3, –2, –1, 0, 1, 2, 3, ...}.
Рациональным называется число, которое можно представить в виде отношения двух целых чисел:  (pÎZ, qÎZ, q¹0). Множество всех рациональных чисел обозначается через Q. Символически определение множества рациональных чисел можно записать так: Q
(pÎZ, qÎZ, q¹0). Множество всех рациональных чисел обозначается через Q. Символически определение множества рациональных чисел можно записать так: Q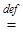 {
{ | pÎZ & qÎZ & q¹0}. Здесь знак
| pÎZ & qÎZ & q¹0}. Здесь знак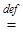 заменяет слово «называется». Заметим, что множество можно задать перечислением элементов, а можно описанием свойств элементов (предикатом), как в последнем случае.
заменяет слово «называется». Заметим, что множество можно задать перечислением элементов, а можно описанием свойств элементов (предикатом), как в последнем случае.
Известно, что любое рациональное число можно представить десятичной дробью, конечной и бесконечной периодической. Например, рациональное число 5/6 представимо бесконечной периодической дробью 5/6 = 0,83333..., а число 3/8 = 0,375. В последнем случае можно считать десятичную дробь тоже бесконечной с числом 0 в периоде: 3/8 = 0,3750000... . Известно, что всякую периодическую бесконечную дробь можно обратить в обыкновенную дробь p/q.
Иррациональным числом называется всякая бесконечная непериодическая десятичная дробь. Множество всех рациональных и иррациональных чисел называется множеством действительных чисел и обозначается через R. Иными словами, множество действительных чисел R – это множество всех бесконечных десятичных дробей.
Пусть M1, M2 – некоторые множества. Если каждый элемент множества M1 является элементом множества M2, то говорят, что M1 есть подмножество множества M2 и обозначается M1 Ì M2. Итак, M1 Ì M2 тогда и только тогда, когда "x(xÎM1 ® xÎM2).
Из определения числовых множеств можно заключить, что N Ì Z, Z Ì Q, Q Ì R. Множество действительных чисел является подмножеством множества C всех комплексных (о которых мы сейчас говорить не будем), т.е. R Ì C.
Часто рассматриваются подмножества действительных чисел (a, b), [a, b], [a, b), (a, b] называемые, соответственно, интервалом, отрезком, полуинтервалом. Дадим символические определения этих множеств, а слово «называется» заменим на знак 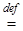 :
:
(a, b) 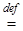 {xÎR| a < x < b}; [a, b]
{xÎR| a < x < b}; [a, b] 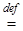 {xÎR| a £ x £ b};
{xÎR| a £ x £ b};
(a, b] 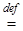 {xÎR| a < x £ b}; [a, b)
{xÎR| a < x £ b}; [a, b) 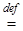 {xÎR| a £ x < b }.
{xÎR| a £ x < b }.
Заметим, что на числовой оси каждое действительное число изображается определенной точкой и любая точка числовой оси задает некоторое число, поэтому [a, b] изображается множеством всех точек отрезка, вместе с концами a, b, в то время как (a, b) – множеством точек отрезка без концов a, b.
Объединение AÈB, пересечение AÇB
Рассмотрим операции множеств A,B давая им символические определения:
AÈB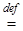 {x| xÎA Ú xÎB}, AÇB
{x| xÎA Ú xÎB}, AÇB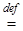 {x| xÎA & xÎB}
{x| xÎA & xÎB}
Иногда рассматривается операция разности множеств A и B, это множество элементов A, не входящие в B. Обозначение: AB. Таким образом, A B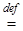 {x|
{x| }. В частном случае R Q есть множество иррациональных чисел.
}. В частном случае R Q есть множество иррациональных чисел.
– Конец работы –
Эта тема принадлежит разделу:
Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности
Данное пособие является составной частью учебного комплекса по курсу высшей математики которое может быть полезно для организации учебного процесса... В учебном пособии рассматриваются следующие темы введение в математический... Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Множества
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов