Предел последовательности

Как отмечалось раньше, любая последовательность a₁, a₂, ..., a_n , ... есть функция натурального аргумента, a_n = f(n), n Î N. Определение предела последовательности почти дословно повторяет определение предела функции при x®+Ґ.

Число b называется пределом последовательности {a_n}, если для любого e > 0 существует такое натуральное число n₀, что для всех натуральных n, больших n₀, выполняется неравенство: | a_n – b | < e. Обозначение: a_n = b.

Доказать самостоятельно, что 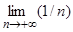= 0.

Предел функции при x® -¥

Пусть функция y = f(x) определена на R или (–¥, a). Число b называется пределом функции f(x) при стремлении x к –¥ (x ® –¥), если для любого положительного числа e существует такое x₀, что для всех x, меньших x₀, выполняется неравенство:
| f(x) – b | < e. Обозначение: f(x) = b.

Геометрически этот факт означает, что точки графика y = f(x) (рис. 1.5) приближаются как угодно близко к соответствующим точкам прямой y = b при движении x влево неограниченно и что по фиксированному e > 0 найдется число x₀, такое, что для всех x, меньших x₀, график y = f(x) заключен внутри полосы, ограниченной прямыми:

y = b + e, y = b – e.

Доказать самостоятельно, что = 0

Рассмотренные пределы объединяются общим названием «пределы на бесконечности». Не надо думать, что любая функция, определенная на R, имеет предел при x ® +¥ или x ® –¥. Например, 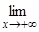sinx не существует, так как значения sinx при неограниченном возрастании x периодически меняются от –1 до +1, не приближаясь ни к какому постоянному числу. Аналогично, не существует sinx. Последовательность: a₁ = 1, a₂ = 3, a₃ = 5, ..., a_n = 2n – 1, ... также не имеет предела.