рефераты конспекты курсовые дипломные лекции шпоры

Раздел Охрана труда
/
Левосторонний и правосторонний пределы функции в точке

Реферат Курсовая Конспект

Выберите учебное заведение

Левосторонний и правосторонний пределы функции в точке

Левосторонний и правосторонний пределы функции в точке - раздел Охрана труда, Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности Переходим К Рассмотрению Односторонних Пределов Функции В Точке X...

Переходим к рассмотрению односторонних пределов функции в точке x₀, при которых переменная x «движется» к x₀ слева (левосторонний предел) или справа (правосторонний предел). Нам потребуется понятие полуокрестности.

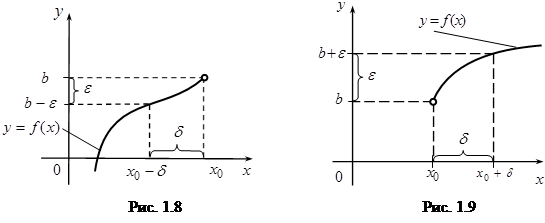
Пусть d > 0. Интервал (a, x₀) называется левой полуокрестностью точки x₀, интервал (x₀– d, x₀) – левой d-полуокрестностью точки x₀. Интервалы (x₀, b), (x₀, x₀+ d) называются, соответственно, правой полуокрестностью и правойd-полуокрестностью точки x₀ (см. рис. 1.8, 1.9).

Пусть f(x₀) определена в левой полуокрестности точки x₀.

Число b называется левосторонним пределом функции f(x) в точке x₀ (обозначение: f(x) = b), если для любого e > 0 найдется d > 0, такое, что для всех значений x, принадлежащих левой d-полуокрестности (x₀ – d, x₀), выполняется неравенство:
|f(x) – b| < e.

Символическиf(x) = b означает: "e>0$d > 0 "x(x₀– d < x < x₀ ® | f(x) – b | < e) (см. рис. 1.8).

Аналогично, число b называется правосторонним пределом функции f(x) в точке x₀ (обозначение: f(x) = b), если для любого e > 0 найдется d > 0, такое, что для всех значений x, принадлежащих правой d-полуокрестности (x₀, x₀+ d), выполняется неравенство: | f(x) – b | < e (см. рис. 1.9).

Символическиf(x) = b означает: "e >0 $d >0 "x(x₀ < x < x₀+ d ® |f(x) – b| < e).

Пример 3. Функция f(x) задана равенством (рис. 1.10):

f(x) = .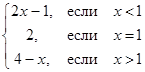

Найти f(x) и f(x).

Решение. Покажем, что f(x) = 1, а f(x) = 3.

Рассмотрим значения x < 1, тогда f(x) = 2x – 1 и | f(x) – 1| = |2x – 1 – 1| = 2|x – 1|. Зафиксируем малое e > 0. Подсчитаем: | f(x) – 1| < e Û 2 |x – 1| < e Û |x – 1| < . Так как x < 1, то
f(x) – 1| < e, если 1 – < x < 1, следовательно, d = . Итак, если 1 – < x < 1, то
| f(x) – 1| < e, т.е. f(x) = 1.

Рассмотрим значения x > 1, тогда f(x) = 4 – x. Зафиксируем e > 0,

| f(x) – 3| = |2 – x – 3| = |1 – x|. Отсюда | f(x) – 1| < e Û |1 – x| < e, т.е. | f(x) – 1 | < e для
x Î (1, 1 + e). Значит, f(x) = 3.

Очевидно, если f(x) = b, то f(x) = b и f(x) = b.

Верно и обратное, если f(x) = f(x) = b, то f(x) = b.

Если же правосторонний предел функции в точке x₀ не равен левостороннему пределу функции в точке x₀, то f(x) = b не существует. Так, в примере 3 функция f(x) не имеет предела в точке x₀.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности

Данное пособие является составной частью учебного комплекса по курсу высшей математики которое может быть полезно для организации учебного процесса... В учебном пособии рассматриваются следующие темы введение в математический... Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Левосторонний и правосторонний пределы функции в точке

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Логическая и математическая символика
В математике употребляются специальные символы, позволяющие сократить запись и точнее выразить утверждение. Математические символы:

Множества
Понятие множества является первоначальным понятием математики, точное определение ему не дается, но его можно пояснить, описать через другие понятия. Можно сказать, что множество

Функции
Пусть x, y – переменные величины. Если каждому значению переменных x из множества A соответствует по определенному закону единственное значение переменной y, то говорят,

Пределы функции на бесконечности
Рассмотрим одно из центральных понятий математического анализа – понятие предела функции. Ввиду сложности для понимания этого понятия сначала дадим его описательное определе

Предел последовательности
Как отмечалось раньше, любая последовательность a1, a2, ..., an , ... есть функция натурального аргумента, an = f(n

Предел функции в точке
Пусть функция f(x) определена в некоторой окрестности точки x0 (возможно, определена на R), но в самой точке x0 функция f(x) м

Бесконечно-малые функции и их свойства
Функция a(х) называетсябесконечно малой (сокращенно: б.м.) при х ® а (х

Основные теоремы о пределах
Теорема 1. Если f(x) = b, то f(x) = b + a(x), где a(x

Доказательство
1) Пусть a – положительный острый угол, докажем= 1. Предварительно докажем, что

Второй замечательный предел
Ранее рассматривались понятия последовательности (как функции натурального аргумента), предела последовательности (см. разд. 1.3, 1.4). Рассмотрим возрастающую последовательность:

Теорема 2 (второй замечательный предел)
Существует предел . Доказательство. Рассмотрим последовательность

Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции
Пусть a(x) и b(x) – б.м. функции при x ® a (x® + ¥, x ® –¥, x ® x0, ...). Рассмотрим предел их отношения при

Доказательство
Пусть a(x) ~ b(x) при x ® a. Тогда =

Непрерывность функции в точке. Точки разрыва
Пусть функция f(x) определена в точке x0 и некоторой ее окрестности. Если существует и

Свойства функций, непрерывных на отрезке
Определение. Если функция f(x) определена на отрезке [a, b], непрерывна в каждой точке интервала (a, b), в точке a непрерывна справа, в точке