рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Охрана труда
- /
- Бесконечно-малые функции и их свойства
Реферат Курсовая Конспект
Бесконечно-малые функции и их свойства
Бесконечно-малые функции и их свойства - раздел Охрана труда, Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности Функция A(Х) НазываетсяБесконечно Малой...
Функция a(х) называетсябесконечно малой (сокращенно: б.м.) при х ® а
(х  + ¥, х ® –¥, x ® x0 – 0, х ® x0 + 0), если
+ ¥, х ® –¥, x ® x0 – 0, х ® x0 + 0), если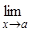 a(х) = 0.
a(х) = 0.
Используя определение предела фикции при х ® +¥, можно перефразировать этог определение: функция a(х) называетсябесконечно малой при х ® +¥, если для любого положительного числа e найдется такое число x0 что для всех х, больших x0, выполняется неравенство: |a(х)|<ε.
Символически это выглядит так: 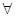 ε > 0
ε > 0 x0
x0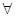
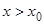 (|
(| (х)|<ε).
(х)|<ε).
Аналогично формулируются определения б.м. при x ® +¥, х ® x0, и т.д.
Пример 1. Функция a(х) = 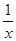 является б.м. при
является б.м. при  и
и 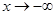 (см. разд. 1.4, пример 3).
(см. разд. 1.4, пример 3).
Пример 2. Покажем, что a(х)= б.м. при
б.м. при  .
.
Действительно, неравенство 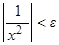 выполняется для всех х, которые удовлетворяют неравенству
выполняется для всех х, которые удовлетворяют неравенству 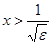 , т.е.
, т.е. 
Докажем некоторые теоремы о б.м. функциях.
Теорема 1. Сумма двух бесконечно малых функций (при ) является б.м. функцией (при
) является б.м. функцией (при ).
).
Доказательство. Проведем доказательство для случая  . Пусть
. Пусть 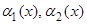 – б.м. при
– б.м. при  , покажем, что функция
, покажем, что функция 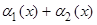 является б.м. при
является б.м. при , т.е.
, т.е.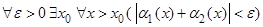 .Зафиксируем произвольное положительное ε. Так как
.Зафиксируем произвольное положительное ε. Так как  – б.м. при
– б.м. при  , то по числу
, то по числу  найдется
найдется  такое, что для всех
такое, что для всех  выполняется неравенство:
выполняется неравенство:
 . (*)
. (*)
Аналогично для  по числу
по числу  найдется
найдется 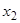 , такое, что для всех
, такое, что для всех  выполняется неравенство:
выполняется неравенство:
 . (**)
. (**)
Пусть x0 – большее из чисел 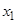 и
и 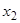 тогда для любого
тогда для любого 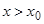 выполняются оба неравенства (*), (**), поэтому
выполняются оба неравенства (*), (**), поэтому  .
.
Учитывая, что 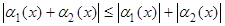 , получаем:
, получаем:
 , т.е.
, т.е.  – б.м. при
– б.м. при 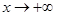 .
.
Пример 3. Функция  является б.м. при
является б.м. при 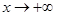 , так как каждое слагаемое
, так как каждое слагаемое 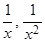 является б.м. при
является б.м. при 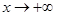 (см. примеры 1, 2).
(см. примеры 1, 2).
Для дальнейшего нам потребуется понятие ограниченности функции.
Функция f(x) называетсяограниченной на некотором множестве М, если существует такое положительное число К, что для всех  М выполняется неравенство:
М выполняется неравенство:  .
.
Пример 4. Функция sinx и cosx ограничены на множестве R всех действительных чисел, так как 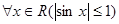 и
и 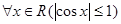 .
.
Пример 5.Функция tgx не является ограниченной на интервале 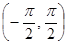 , так как она может принимать любые значения при
, так как она может принимать любые значения при  .
.
Будем говорить, что функция f(x) ограничена при 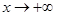 (
( ), если она ограничена на некотором бесконечном интервале (
), если она ограничена на некотором бесконечном интервале (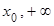 ) (или (
) (или ( )). Аналогично, функцию f(x) называют ограниченной при
)). Аналогично, функцию f(x) называют ограниченной при  (
( ), если она ограничена на некоторой окрестности (
), если она ограничена на некоторой окрестности ( ) точки
) точки  (на правой полуокрестности (
(на правой полуокрестности (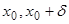 ) или на левой полуокрестности (
) или на левой полуокрестности (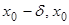 ) соответственно).
) соответственно).
Теорема 2. Если существует  f(x), то функция f(x) ограничена при х
f(x), то функция f(x) ограничена при х  а.
а.
Доказательство. Проведем доказательство для случая 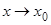 .
.
Пусть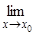 f(x) = b. Тогда на основании определения предела для ε = 1 найдется такое δ > 0, что для всех x, удовлетворяющих условию
f(x) = b. Тогда на основании определения предела для ε = 1 найдется такое δ > 0, что для всех x, удовлетворяющих условию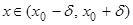 , выполняется неравенство: |f(х) – b| < 1. Так как по свойству абсолютных величин
, выполняется неравенство: |f(х) – b| < 1. Так как по свойству абсолютных величин 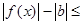 |f(х) – b|, то
|f(х) – b|, то
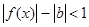 , откуда |f(х)| < |b| + 1.
, откуда |f(х)| < |b| + 1.
Это и означает, что f(х) ограничена на интервале ( ) (в качестве К взято число |b| + 1).
) (в качестве К взято число |b| + 1).
Следствие 1. Любая б.м. функция при  является ограниченной при
является ограниченной при  .
.
Теорема 3. Если существует 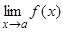 и он отличен от нуля, то
и он отличен от нуля, то  ограничена при
ограничена при  .
.
Доказательство.Пусть f(x) = b
f(x) = b  0. Зафиксируем положительное число ε, такое, что ε <
0. Зафиксируем положительное число ε, такое, что ε <  . На основании определения предела при
. На основании определения предела при 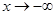 :
:
 .
.
Так как
 , то
, то 
 и
и 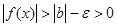 .
.
Следовательно,  . Здесь К =
. Здесь К = 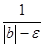 . Теорема доказана.
. Теорема доказана.
Теорема 4. Произведение б.м. функции (при х  а) на функцию, ограниченную (при х
а) на функцию, ограниченную (при х  а) является функцией б.м. (при х
а) является функцией б.м. (при х  а).
а).
Доказательство. Пусть функция  (х) – б.м. при
(х) – б.м. при  , и пусть f(х) – ограничена при
, и пусть f(х) – ограничена при  , т.е. найдутся числа К > 0 и x1, такие, что для любого х > х1 выполняется неравенство:
, т.е. найдутся числа К > 0 и x1, такие, что для любого х > х1 выполняется неравенство:
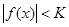 . (!)
. (!)
Зафиксируем произвольное ε > 0 и покажем, что найдется x0, такое, что 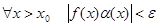 .
.
По определению б.м. при 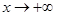 , для числа
, для числа  найдется такое x2, что для всех
найдется такое x2, что для всех
х > х2, выполняется неравенство:
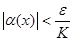 . (!!)
. (!!)
Пусть  – наибольшее из чисел х1, х2. Тогда для х > x0 одновременно выполняются неравенства (!), (!!), поэтому
– наибольшее из чисел х1, х2. Тогда для х > x0 одновременно выполняются неравенства (!), (!!), поэтому
 ,
,
т.е. f(х)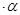 (х) – б.м. при
(х) – б.м. при 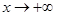 . Теорема доказана.
. Теорема доказана.
Следствие 2. Произведение функции б.м. при 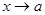 на число является функцией б.м. при
на число является функцией б.м. при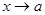 .
.
Следствие 3. Произведение двух б.м. функций есть функция б.м. (при 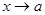 ).
).
Замечание. Если  1(х),
1(х),  2(х) – б.м. при
2(х) – б.м. при 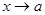 , то
, то 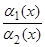 может быть б.м. при
может быть б.м. при 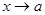 , а может и не быть. Так, для функций
, а может и не быть. Так, для функций  1(х) =
1(х) = 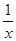 и
и  2(х) =
2(х) =  , б.м. при
, б.м. при  , функция
, функция  не является б.м. при
не является б.м. при  , а функция
, а функция  является б.м. при
является б.м. при  .
.
1.7. Бесконечно большие функции, их свойства и связь
с бесконечно малыми функциями
Функция F(x) называется бесконечно большой (сокращенно б.б.) при x ® +¥
(при x ® -¥), если для любого положительного числа K существует число x0, такое, что для всех x > x0 выполняется неравенство: |F (x)| > K.
Функция F(x) называется бесконечно большой при x ® x0 (при x ® x0–0 или
x ® x0+0 ), если для любого K > 0 существует d > 0 такое, что для любого
xÎ(x0 – d, x0 + d), ("xÎ(x0 – d, x0) или "xÎ(x0, x0 + d) соответственно) выполняется неравенство |F(x)| > K.
Очевидно, что всякая бесконечно большая функция не является ограниченной при
x ® a, а потому  F (x) не существует.
F (x) не существует.
Если F (x) – б.б. функция при x ® a, то говорят, что F (x) стремится к бесконечности и пишут:  F (x) = ¥. Если при этом F (x) > 0, то пишут:
F (x) = ¥. Если при этом F (x) > 0, то пишут:  F (x) = +¥; если же F(x) < 0, то пишут:
F (x) = +¥; если же F(x) < 0, то пишут:  F (x) = -¥.
F (x) = -¥.
Пример 1. F1(x) = x2 является б.б. при x ® +¥ и x ® -¥, причем F1(x) > 0, поэтому можно записать: x2 = + ¥,
x2 = + ¥,  x2 = + ¥.
x2 = + ¥.
Пример 2. F2(x) = 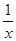 является б.б. при x ® 0, причем
является б.б. при x ® 0, причем
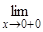 F2(x) = +¥, а
F2(x) = +¥, а  F2(x) = - ¥.
F2(x) = - ¥.
Следующие две теоремы устанавливают связь между бесконечно большими и бесконечно малыми функциями.
Теорема 1. Если функция F(x) является б.б при x ® a, то функция  – б.м. при x ® a.
– б.м. при x ® a.
Доказательство. Пусть F(x) – б.б. при x ® x0–0, покажем, что  – б.м. при
– б.м. при
x ® x0–0. Зафиксируем произвольное e > 0 и покажем, что найдется d > 0 такое, что для всех xÎ(x0 – d, x0) выполняется неравенство: | | < e.
| < e.
По определению функции б.б. при x ®x0–0 для числа K = 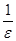 найдется такое d > 0, что "xÎ(x0–d, x0) будет выполняться неравенство: |F(x)| >
найдется такое d > 0, что "xÎ(x0–d, x0) будет выполняться неравенство: |F(x)| > 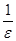 , откуда
, откуда  < e для
< e для
xÎ(x0 – d, x0), т.е.  – б.м. при x ® x0 –0.
– б.м. при x ® x0 –0.
Теорема 2. Если a(x) – б.м. при x ® a и a(x) ¹ 0, то  – б.б. при x ® a.
– б.б. при x ® a.
Доказательство. Доказательство аналогично предыдущему.
Теоремы 1 и 2 позволяют получить свойства б.б. функций, аналогичные свойствам б.м. функций.
Свойство 1. Если F1(x), F2(x) – б.б. при x ® a, то функция F1(x), F2(x) – б.б. при x ® a.
Свойство 2. Если F1(x), F2(x) – б.б. функции при x®a, причем F1(x) > 0 и
F2(x) > 0 (т.е.  F1(x)=+¥,
F1(x)=+¥,  F2 (x) = + ¥), то функция F1(x) + F2(x) – б.б. при x ® a.
F2 (x) = + ¥), то функция F1(x) + F2(x) – б.б. при x ® a.
Свойство 3. Если F(x) – б.б. при x ® a и число C ¹ 0, то CF(x) – б.б. при x ® a.
Замечание. Если F1(x) и F2(x) – б.б. функции при x ® a, но имеют разные знаки, то F1(x) + F2(x) может быть как б.б., так и б.м. при x ® a, как иметь предел при x ® a, так и не иметь его.
– Конец работы –
Эта тема принадлежит разделу:
Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности
Данное пособие является составной частью учебного комплекса по курсу высшей математики которое может быть полезно для организации учебного процесса... В учебном пособии рассматриваются следующие темы введение в математический... Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Бесконечно-малые функции и их свойства
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов