Г л а в а 2

МИНИМИЗАЦИЯ ПРЕДСТАВЛЕНИЙ БУЛЕВЫХ ФУНКЦИЙ

 

Одной из важнейших задач, возникающих при синтезе переключательных схем, является минимизация представления БФ путем тождественных преобразований.

Представление БФназывается минимальным, если оно включает минимальное количество вхождений букв (обозначений переменных) по сравнению с другими эквивалентными представлениями.

В настоящее время при решении практических задач синтеза переключательных схем пользуются различными алгоритмами упрощения представлений БФ. Необходимо отметить, что применение любого из алгоритмов не гарантирует получения минимальных форм, но позволяет достаточно эффективно получать формы, близкие к минимальным. Это обусловлено тем, что упрощение может быть достигнуто различными путями. Кроме того, неоднозначно определяется минимальное представление функций алгебры логики. Одна и та же функция может иметь несколько минимальных форм. Так, например, для функции

существуют две эквивалентные минимальные ДНФ:

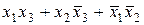и .

Чаще всего упрощение представления БФ осуществляется посредством использования в различной последовательности и интерпретации свойств склеивания и поглощения.

Мы ограничимся рассмотрением двух распространенных способов минимизации представления БФ: минимизации с помощью карт Карно и метода неопределенных коэффициентов. Представление БФ с помощью карт Карно является одним из самих наглядных и позволяет оценить расположение функции в пространстве, а метод неопределенных коэффициентов наиболее формализован и удобен для программирования.

 

2.1. Карты Карно

Карта Карно (КК) является графическим способом представления БФ и получения упрощенных выражений. Таблица истинности функции, зависящей от любого количества переменных, является двумерным представлением БФ и часто не позволяет произвести возможные упрощения. КК представляет таблицу истинности в пространстве. КК для двух, трех и четырех переменных приведены на рис. 2.1.

 

 

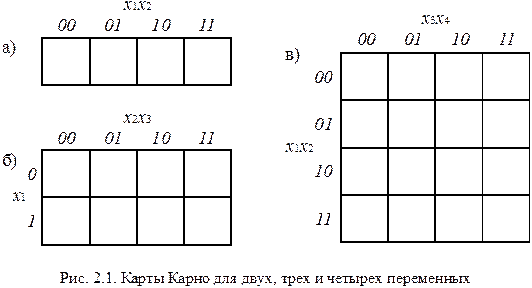
Каждая из клеток соответствует одной из комбинаций 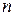переменных. КК организованы таким образом, что соседние по строке или по столбцу клетки отличаются значением только одной переменной. При этом полагают, что крайние строки и столбцы таблицы считаются соседними, как если бы фигура была размещена на торе.

Для упрощения обозначений строки и столбцы, содержащие некоторую переменную, равную 1, обозначают фигурной скобкой, так что значение 0 эта переменная будет иметь в неотмеченных местах (рис. 2.2).

 

 

Чтобы представить БФ на карте, достаточно в те клетки, где функция имеет значение 1, поместить единицы. Тогда в остальных клетках будут содержаться нули. На рис. 2.3 изображена КК для БФ

.

 

 

Клетки, в которых записаны 1, называют р-клетками БФ, так как 1 представляет собой произведение всех переменных (некоторые могут быть с отрицанием). Две соседние единицы образуют одномерный р-подкуб (рис. 2.4). Этот одномерный р-подкуб может быть представлен простым произведением, содержащим одну переменную 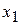, так как два вхождения 1 в этом подкубе соответствуют и 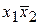; таким образом свойство поглощения +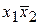=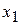проверено графически. На рис. 2.5 этот принцип применен к БФ от трех переменных, изображенной на рис. 2.3. В соответствии с тремя выделенными подкубами можно упростить БФ следующим образом:

.

В общем случае одномерный р-подкуб соответствует произведению, в котором всегда отсутствует одна переменная (или ее отрицание). Переменную, отсутствующую в произведении, также легко определить по карте, это будет та переменная, которая имеет различные значения для двух единиц соответствующего подкуба. Так , на рис. 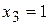2.5 в левом подкубе для левой единицы , а для правой единицы (отсутствует ), в правом подкубе для левой единицы , а для правой единицы (отсутствует ), в вертикальном подкубе для верхней единицы 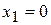, а для нижней единицы 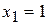(отсутствует ).

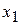Четыре соседние единицы (рис. 2.6) называют двумерным р-подкубом; каждый из них соответствует произведению без двух переменных (во втором примере все четыре единицы являются соседними, так как карты, как пояснялось выше, можно сворачивать). Опущены те переменные, которые не сохраняют постоянное значение на этом подкубе. Аналогично трехмерные р-подкубысодержат восемь единиц (рис 2.7).

 

 

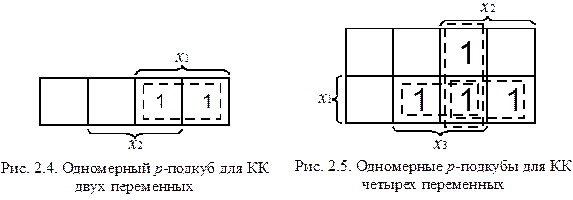
Представление, полученное путем выбора р-подкубов функции, дает ее выражение в ДНФ. Чем больше размерность р-подкубов и чем меньшее число их использовано, тем проще получается ДНФ. Дальнейшее упрощение можно получить за счет вынесения переменных за скобки.

 

 

 

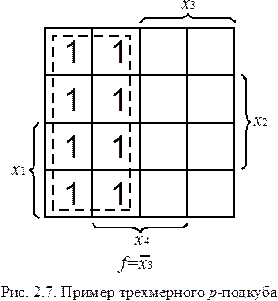
Принимая во внимание клетки КК, не содержащие единиц, и поступая с ними так же, как с клетками с единицами, можно представлять функции в КНФ. Пример подобного представления для БФ из рис. 2.5 приведен на рис. 2.8.

Таким образом, инверсию 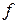можно выразить как

.

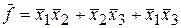На основе правила де Моргана функцию 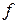можно представить в виде .

 

 

 

КК удобно использовать для минимизации представления БФ, при задании которой использовались безразличные комбинации. Безразличные условия позволяют придать функции те значения, которые приводят к упрощению синтезируемой функции (или реализующей ее схемы).

Согласно договоренностям, принятым в разделе 1.3, безразличные комбинации будут обозначаться в КК символом d. В любые клетки, имеющие d, для увеличения размеров р-подкубов можно помещать единицы. На рис. 2.9 изображена КК для функции с безразличными значениями, заданной табл. 1.9. Доопределим ее (рис 2.10).

 

 

 

 

 

 

 

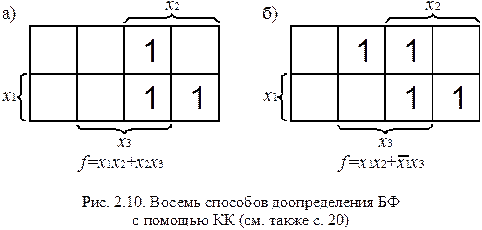
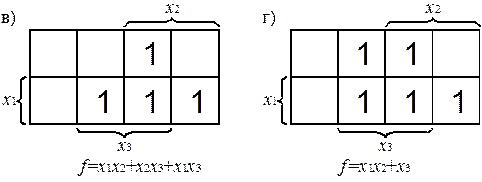
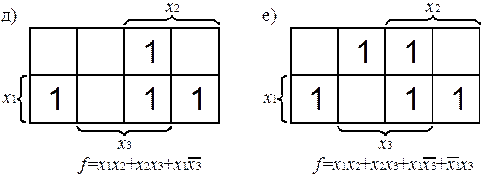
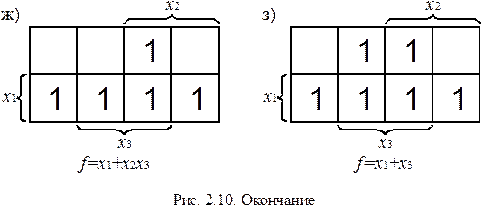
Так как данная БФ имеет три безразличных значения, ее можно доопределить восемью способами. Очевидно, что минимальный вид БФ принимает при доопределении всеми единицами (рис. 2.10, з).