Математическое описание.
Как правило, математическая модель САУ является дифференциальным или интегрально-дифференциальным уравнением. Уравнения бывают двух видов:
1) уравнение динамики (переходные процессы)
2) уравнение статики (статические характеристики)
Уравнения статики получают из уравнения динамики. Для этого все производные сигналов приравнивают к нулю, либо к постоянной (const). В результате уравнение опишет связь между входом и выходом.
ώ
ώ1
Статическая характеристика
U1 U
Для составления математической модели САУ ее разбивают на отдельные элементы, для каждого из которых легко составляется и находится собственное уравнение. При этом необходимо учесть, что входной сигнал на какой-то элемент, есть выходной с предыдущего.
Поэтому получается система уравнений, решая которую получается математическая модель САУ, которая зависит от входного сигнала или выходного.
Методика составления математической модели:
1. После разбивания на отдельные элементы необходимо для каждого элемента выявить тот физический закон, который определяет его поведение. Это закон Ньютона, закон сохранения энергии и другие фундаментальные законы физики. Запись осуществляется в дифференциальной форме, например: F = ma, F = m 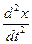
2. Определяются факторы, от которых зависят переменные, входящие в исходное уравнение и установленное выражения, характеризующего эту зависимость. Эти зависимости могут быть выражены аналитически или графически. Подстановка их в исходное уравнение дает нам, как правило, нелинейное уравнение элемента САУ, после чего, чаще всего, проводят линеаризацию, т.е. замену реальных свойств на упрощенные линейные зависимости. Но линеаризация должна быть допустимой.
Формы записи нелинеаризованных уравнений САУ
Линеаризованное дифференциальное уравнение:
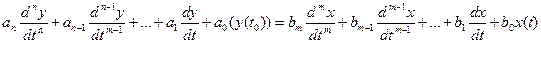
где: y(t), x(t) – выходная и входная величины элемента
an, bn – постоянные коэффициенты
n – порядок уравнение, (n≥m)
Данное уравнение получается из решения системы уравнений.
Введем символ дифференцирования p = 
(anpn+an-1pn-1+…+a1p+a0), y(t)
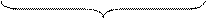
D(P)
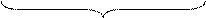 (bmpm+bm-1pm-1+…+b0), x(t)
(bmpm+bm-1pm-1+…+b0), x(t)
N(P)
D(P) и N(P) – полиномы
D(P)y(t) = N(P)x(t)
Для записи уравнений САУ используют несколько разных форм.
Выходные величины и ее производные = Выходные величины и все остальные члены
Выходная величина y(t) должна иметь коэффициент равный 1
Разделим левую и правую части на a0:
(TnPn+Tn-1pn-1+…+T1p1+1)y(t) = (kmpm+km-1pm-1+…+k1p1+k0)x(t)
Все коэффициенты Tn…T1 – постоянные времени. Измеряются в [c], характеризуют инерционные свойства системы.
km – коэффициент передачи.
Вторая стандартная форма записи.
Для нее применяют операторный метод или метод Лапласа. Решение дифференциальных уравнений сводится к алгебраическим действиям. В дифференциальном уравнении:
1) вместо реальных функций времени записать их изображения по Лагранжу;
2) в полиномах символ дифференциала P заменить на оператор Лапласа S
применим преобразование Лапласа:
D(S)Y(S)=N(S)X(S) + M(S)F(S)
Где S – оператор Лапласа (полином)
Y(S), X(S), F(S) – изображения по Лапласу выходной и входной величин элемента и внешнего воздействия
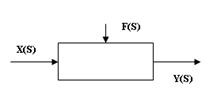
F(S) – дополнительный вход
Так как в реальных системах входов может быть много, то много и слагаемых. Однако, при анализе САУ применяют принцип суперпозиции. Он означает, что реакция системы (выход) представляет собой сумму реакций на каждом из входных воздействий. Поэтому можно рассматривать САУ последовательно с каждым входом.
Оператор Лапласа представляет собой комплексную величину:
S = c*jώ
с = Res – абсцисса абсолютной сходимости; вещественная часть комплексного числа.
Для перехода от реальной функции времени – оригиналов к их изображениям по Лапласу и наоборот вводят прямое интегральное преобразование

Обратное интегральное преобразование

В результате преобразований Лапласа мы получаем алгебраическое уравнение изображения функции времени по Лапласу.
Введем обозначения:
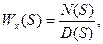
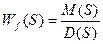 - передаточные функции по входному сигналу x и f
- передаточные функции по входному сигналу x и f
Передаточная функция – отношение изображения выходного сигнала к входному.

Если индекса у функций нет, то предполагается, что есть только один входной сигнал X.
Так как выходной сигнал, как правило, нам известен или мы можем его задать в виде входного типового воздействия свойства системы, также известны (передаточная функция), то всегда стоит вопрос о нахождении изображения выходного сигнала.

Данную форму записи можно представить в виде структурной схемы:

Для того, чтобы применить преобразование Лапласа удобнее всего пользоваться специальными таблицами.
Данные таблицы применяются для так называемых причинных систем.
Причинная система – это динамическая система, для которой выполняется принцип причинности, т.е. выход такой системы Y(T) в какой-то момент времени t0 зависит только от значения входного сигнала x(t) в момент времени t меньше и равным моменту t0. Таким образом, в таких системах вектор фазовых координат и выходное значение зависит только от прошлого и текущего значения выходного сигнала.
В реальном мире все системы являются причинными.
S – корни характеристических уравнений.