Математическая база параметрической стандартизации

Многообразие типов, параметров и размеров изделий регламентируется параметрическими стандартами. Тем самым предотвращается воз­можность производства неоправданно большой номенклатуры изделий в той или иной отрасли промышленности, создаются благоприятные условия для широкой унификации деталей и узлов, для развития предметной и подетальной специализации и для облегчения эксплуатации и ремонта из­делий, в частности, проще решается проблема запасных частей. Согласо­вание параметров и размеров методом параметрической стандартизации позволяет увязать между собой различные отрасли промышленности, проще решается проблема запасных частей. Это дает большой экономический эффект в масштабе всего народного хозяйства страны.

Сущность параметрической стандартизации состоит в том, что параметры и размеры серийно выпускаемых изделий устанавливаются не произвольно, а в соответствии с рядами предпочтительных чисел, т. е. таких чи­сел, которым предписывается отдавать предпочтение по сравнению со все­ми другими. Примеры использования предпочтительных чисел встречают­ся повсюду: размеры одежды и обуви, длина гвоздей, диаметры болтов и внутренних отверстий гаек, номинальные значения массы гирь, мощности машин и т. д.

Предпочтительным числам свойственны определенные математические закономерности. Так, наипростейшие ряды предпочтительных чисел строят­ся на основе арифметической прогрессии, т. е. такой последовательности чисел, в которой разность между последующим и предыдущим членами (она называется разностью прогрессии) остается постоянной. Любой член арифметической прогрессии можно вычислить по формуле:

a_n = a₁ + d(n-1)

где а₁ — первый член прогрессии, d — разность прогрессии, п — номер взятого члена.

Ряды предпочтительных чисел, основанные на арифметической прог­рессии, используются в параметрических стандартах сравнительно редко, однако такие стандарты есть. Это, например, стандарты на диаметры под­шипников качения, стандарты на размеры обуви. Достоинством рядов предпочтитель­ных чисел, базирующихся на арифметической прогрессии, является их простота, недостатком - относительная неравномерность. Так, в примере возрастающей арифметической прогрессии с разностью 1 второй член превышает первый на 100 %, десятый больше девятого на 11 %, а сотый больше девяносто девятого всего на 1 %. В результате большие значения следуют сравнительно чаще друг за другом, их оказывается больше, чем маленьких, что отнюдь не всегда рационально и соответствует потребнос­тям народного хозяйства.

Для преодоления этого недостатка используют отрезки рядов, пост­роенных на основе арифметической прогрессии, с большими номерами, где неравномерность выражена менее, или используют ступенчато-арифметические прогрессии. Такую прогрессию образуют, например, достоинства монет.Ступенчатая арифмети­ческая прогрессия у нас в стране была использована для параметрической стандартизации еще в 1717 г., когда по указу Петра I установили калибры ядер: 4, 6, 8, 12, 18, 24, 36.

С древнейших времен для построения рядов предпочтительных чисел использовалась геометрическая прогрессия, т. е. такая последователь­ность чисел, в которой отношение последующего к предыдущему члену (оно называется знаменателем прогрессии) остается постоянным. Приме­рами геометрической прогрессии являются последовательности:

а) возрастающая со знаменателем 1,1: 1—1,1—1,21—1,33—

б) убывающая со знаменателем 0,1: 1-0,1-0,01-0,001- .... Любой член геометрической прогрессии можно вычислить по фор­муле:

а_n =a₁ q^n-1

где a₁ — первый член, q — знаменатель прогрессии; n — номер взятого члена.

Геометрическая прогрессия имеет ряд полезных свойств, используемых в стандартизации.

1. Относительная разность между любыми соседними членами ряда
постоянна. Это свойство вытекает из самой природы геометрической
прогрессии. Возьмем в качестве примера простейшую прогрессию со знаме­нателем, равным двум:

1-2- 4-8-16-32-64 - здесь любой член прогрессии больше предыдущего на 100 %.

2, Произведение или частное любых членов прогрессии является членом той же прогрессии. Это свойство используется при увязке между со­бой стандартизуемых параметров в пределах одного ряда предпочтительных чисел. Согласованность параметров является важным критерием качест­венной разработки стандартов. Геометрические прогрессии позволяют сог­ласовывать между собой параметры, связанные не только линейной, но также квадратичной, кубичной и другими зависимостями.

Ряды предпочтительных чисел должны удовлетворять следующим тре­бованиям:

1) представлять рациональную систему градаций, отвечающую потребностям производства и эксплуатации;

2) быть бесконечными как в сторону малых, так и в сторону боль­ших значений, т.е. допускать неограниченное развитие параметров или размеров в направлении их увеличения или уменьшения;

3) включать все десятикратные значения любого члена и единицу:

4) быть простыми и легко запоминающимися.

Специальные исследования показали, что всем этим требованиям наилучшим образом удовлетворяют геометрические прогрессии с десятикратным увеличением каждого к-го члена. Из условия

а_п = 10a получаем aq^п =10 а, откуда q =.

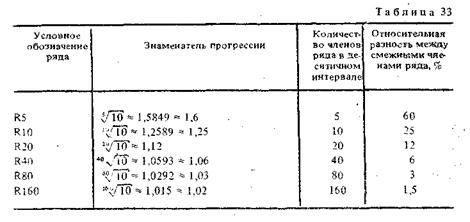
ГОСТ 8032-84 устанавливает четыре основных ряда предпочтительных чисел и два дополнительных (R80 и R160), применение которых допус­кается только в отдельных, технически обоснованных случаях. Краткие сведения об этих рядах приведены в табл. 3.1(34). На примере этой таблицы рассмотрим некоторые свойства основных рядов предпочтительных чисел.

1. ГОСТ 8032-84 устанавливает стандартные значения предпочтитель­ных чисел в диапазоне 0<а< ∞ на основе фиксированных значений пред­почтительных чисел, включенных в десятичный интервал 1 ≤а < 10.

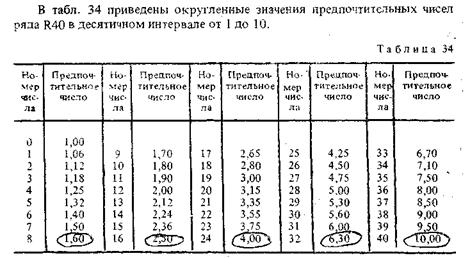
Все эти числа, включенные в ряд R40, приведены в табл. 3.2(34)

Для перехода от предпочтительных чисел, приведенных в табл. 34, в любой другой десятичный интервал нужно умножать эти числа на 10^к, где к — целое положительное (или отрицательное) число, определяю­щее отдаление десятичного интервала в ту или другую сторону от задан­ного, принятого за нулевой (к= 0).

Так, при к — 1 числа переходят в интервал 10 < а < 100, при

к = — 1 — в интервал 0,1 <а< 1 и т. п.

Практически умножение предпочтительных чисел на 10^к сводится к переносу запятой, входящей в каждое число табл. 34, на к знаков впра­во (при +к) или влево (при —к).

Приведем примеры образования стандартных предпочтительных чисел в разных десятичных интервалах:

5,00* 10³ =5000; 1,18* 10^-2 =0,0118; 3,75 *10 = 37,5.

2. Номер ряда предпочтительных чисел (R40, R20, R10, R5) указывает на количество чисел в десятичном интервале, Так, ряд R40 содержит в десятичном интервале 40 чисел.

Число 1,00, имеющееся в табл, 34, не входит в десятичный интервал 1 < а < 10. Его можно рассматривать как завершающее число предыдущего десятичного интервала 0,1 <а < 1,

3. Таблица включает все основные ряды предпочтительных чисел, В
ней нетрудно найти числа, образующие ряды R 5, R10, R20,

Для примера построим ряд R5, Здесь полезно напомнить одно из
требований к рядам предпочтительных чисел: они должны включать единицу. С единицы и начнем, включив ее в отрезок ряда R5 (в табл. 34 единица имеет нулевой номер), Чтобы получить следующее число ряда, нужно умножить единицу на знаменатель прогрессии q = 1,60. Найдем искомое число под номером 8.

Дальнейшее последовательное умножение найденных чисел на q и округление полученных значений (округления во всех рядах R приняты одинаковыми) приведут к ряду R5:1-1,6-2,5-4,0-6,3-10,0-16,0- … ,

Таблица построена так, что все числа ряда R5 оказались в нижней ее строке (будем называть ее восьмой строкой — по номеру числа в первом столбце). Нетрудно видеть, что в десятичном интервале 1 < а < 10 ряд R5 содержит пять чисел.

Аналогично находим в таблице числа рядов R10 и R20, Начинаем в обоих случаях с единицы и умножаем числа на соответствующие знамена­тели прогрессии.

Ряд R10 имеет вид: 1-1,25-1,60-2,00-3,15-4,00-5,00-6,30-8,00-10,00-12,50- ...

Легко обнаружить, что все эти числа входят в четвертую и восьмую строки таблицы. Десятичный интервал 1 <а < 10 содержит 10 чисел.

Числа ряда R20 .входят, во все четные строки таблицы: вторую, чет­вертую, шестую и восьмую. В.десятичном интервале 1 < а < 10 ряда R20 будет, как и следовало ожидать, двадцать чисел.

4. В табл. 34 есть число 3,15, которое стандартизаторы используют в
своей практике в качестве числа π = 3,1416, Неточность, вносимая при
этом, не превышает 0,03 %, что находится внутри принятого -диапазона
округлений для ряда R40.

Использование при расчетах числа π позволяет выражать предпочтительными числами длины окружностей, площади кругов, угловые скорос­ти, скорости резания, цилиндрические и сферические поверхности и объе­мы, При этом используется свойство геометрических прогрессий: произ­ведение членов прогрессии является членом той же прогрессии. Так, если выразить диаметр окружности D предпочтительным числом, например, ряда R 40,и умножить это число на другое предпочтительное число 3,15, то длина окружности /= πD будет представлена предпочтительным числом того же ряда,

Число π в стандартизации применяется для согласования параметров и размеров, связанных между собой не только линейными или степен­ными зависимостями,

5. В табл. 34 все предпочтительные числа ряда R40 имеют номера от 0 до 40. Эти номера облегчают стандартизаторам расчеты взаимосвязан­ных показателей стандартов, ускоряют вычисление.

Обратим внимание на то, что номера чисел N представляют собой
логарифмы предпочтительных чисел а при основании логарифмов, равном знаменателю прогрессии q:

N=log_q a,

В самом деле, знаменатель прогрессии ряда R40 равен q = 1,06, Оче­видна логарифмическая связь между номерами предпочтительных чисел и соответствующими предпочтительными числами:

q⁰ = 1; qⁱ = 1,06; q² = 1,12; . . . ; q⁴⁰= 10.

В практике вычислений для упрощения расчетов используется извест­ное свойство логарифмов, позволяющее вместо умножения или деления самих предпочтительных чисел складывать или соответстввнно вычитать номера этих чисел, а по результирующему номеру определять искомое число, Это дает кроме ускорения вычислений возможность оперировать с округленными числами и позволяет определять стандартный результат расчетов, без дополнительных округлений,

Например, если непосредственно перемножать предпочтительные чис­ла 2,24 и 3,55, то получим 7,952; результат требуется округлить, привес­ти его к стандартному значению 8,00. При использовании же номеров пред­почтительных чисел (см, табл, 34) достаточно выполнить сложение:

N = N_2,24 +N_3,55 =14 + 22 = 36.

Под номером 36 значится стандартное число 8,00. При переходе от таб­лицы в другие десятичные интервалы, т, е, при умножении чисел на 10^k, номера чисел последовательно нарастают при +к (от 41 и выше), а при —к по мере удаления от предпочтительного числа 1 номера чисел растут по абсолютному значению, но имеют отрицательные знаки (0, — 1, -2, -3, и ,.. т, д.)

Приведенные в табл. 33 ряды не ограничены никакими пределами. Ря­ды с ограниченными пределами обозначаются следующим образом:

R40(15 . . . 190) — основной ряд R40, ограниченный членом 15 в качест­ве нижнего предела и членом 190 в качестве верхнего предела;

R20(22,4 . . .) — основной ряд R20, ограниченный членом 22,4 в качест­ве нижнего предела;

R10(. . . 50) — основной ряд R10, ограниченный членом 50 в качестве верхнего предела;

R20(100 . . . 250) - основной ряд R20 с округленными членами, ограниченный снизу и сверху числами 100 и 250 и содержащий замену чле­нов, входящих в этот диапазон ряда, величинами первой степени округ­ления.

В стандартизации используют также производные ряды. Они применяются в тех случаях, когда ни одна из градаций основных рядов не удов­летворяет поставленным требованиям. Обычно по производным рядам строят ряды параметров и размеров, являющихся функциями других па­раметров и размеров, для которых градации приняты по основным рядам. Производные ряды образуются из основных (или дополнительного) путем отбора каждого второго, третьего или, в общем случае, n-го члена ря­да.

В обозначении производного ряда после наклонной черты указывается порядковый номер систематически отбираемого из ряда члена:

R40/5( . . . 60) — производный ряд, полученный путем отбора каждого пятого члена основного ряда R40 и ограниченный членом 60 в ка­честве верхнего предела; R10/3 ( . . . 80 . . . ) — производный ряд, образо­ванный отбором каждого третьего члена ряда R10 с обязательным вклю­чением члена 80, пределами не ограничен;

- R20/3 (14 . . . 40) — производ­ный ряд, полученный путем отбора каждого третьего члена основного ряда R20 и ограниченный сверху и снизу соответственно членами 40 и 14. Нетрудно убедиться, пользуясь табл. 34, что последний производный ряд содержит 4 члена: 14—20—28—40.

Предпочтительные числа, включенные в ГОСТ 8032—84, как уже отме­чалось, являются округленными по сравнению с расчетными числами гео­метрических прогрессий. Однако, как показывает практика, в отдельных случаях требуются дополнительные округления стандартизованных чисел. Например, при установлении числа зубьев шестерен нельзя использовать число 31,5 (типичным может быть 32), или нецелесообразно требовать вре­мени экспозиции для фотоаппаратов 1/31,5 с вместо более простого зна­чения 1/30 с (число 3,00 отсутствует в рядах R5, R10, R20). Иногда необ­ходимость в дополнительных округлениях вызывается неготовностью производства к применению предпочтительных чисел. В подобных слу­чаях лучше иметь стандартизованные округленные числа, чем допускать применение всевозможных непредпочтительных чисел. В дальнейшем это позволит облегчить переход к применению предпочтительных чисел.

В радиоэлектронике параметрические стандарты приведены в соответствие с рекомендациями Международной электротехнической комиссии (МЭК). Этими рекомендациями установлены предпочтительные числа по рядам ЕЗ, Е6, Е12, Е24, Е48, Е96 и Е192. Наиболее широкое применение имеют первые четыре. Они построены на базе геометрических прогрессий со следующими знаменателями:

для ряда ЕЗ q = = 2,2,

дая ряда Е6 q= = 1,5,

для ряда Е12 q= = 1,2,

для ряда Е24 q= 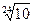= 1,1.

В табл.3.3(35) приведены числа ряда Е24 в десятичном интервале 1 < а <10

.

Табл. 35 построена аналогично табл. 34. В последнюю строку таблицы входятвсе числа ряда E6 (в десятичном интервале 1 < а < 10). Строка, начинающаяся с члена 1,2 (знаменатель прогрессии ряда Е12), и послед­няя строка включают в себя двенадцать чисел ряда Е12.

В отличие от рядов R в рядах Е24, Е12, Е6 дается только один знак после запятой (только десятые доли чисел). Из этого следует, что округ­ленные значения членов прогрессии, принятые в качестве стандартных пред­почтительных чисел, в большейстепени отличаются от расчетных значений, чем в рядах R.