Метод половинного деления.

Метод деления отрезка пополам всегда приводит к искомому результату, но иногда он требует значительного объема вычислительной работы. Поэтому обычно его используют, когда возникают трудности с оценкой погрешности в других методах.

 

Рис.3.10.1.

 

Суть метода половинного деления заключается в следующем. Разделим отрезок [ p, s ], на котором ищем корень, пополам, т.е. возьмем и проверим, если | F(y_H) | <=Е_З, то корень уравнения найден. Если же |F(y_Н)| >Е_З, то выберем тот из отрезков [а,у_Н] или [у_Н, b], на концах которого функция F(y) имеет противоположные знаки, и снова разделим его пополам. Этот процесс повторяется до тех пор, пока текущая погрешность не станет меньше заданной. Очевидно, что до начала решения надо убедиться, что корень уравнения располагается на отрезке [ p, s ]. Фрагмент алгоритма решения уравнения методом половинного деления приведен на рис.3.10.1.

В данном случае целесообразно вычисление функции F(Y) оформить в виде подпрограммы-функции (FY() на рис.3.10.1) с одним фактическим параметром – значение Y, для которого надо вычислить значение функции. Достоинством такого способа вычисления значения функции является высокая степень общности алглритма – для решения того или иного уравнения достаточно записать это уравнение в одном месте – в подпрограмме функции FY. Например, если надо решать уравнение

,

то алгоритм подпрограммы FY будет иметь вид приведенный на рис.3.10.2. При этом предполагается, что параметры а и b уравнения передаются в подпрограмму как глобальные переменные.

 

В алгоритме рис.3.10.1 сначала осуществляется проверка (блок 1) существования корня на интервале [ p, s ] – для этого произведение функций на концах интервала должно быть отрицательным. Если произведение функций положительно, то признак ER получает значение 1 и осуществляется выход из алгоритма. Значение ER=1 соответствует ситуации "Корень вне заданного интервала". Затем осуществляется проверка значений функции на концах интервала (блоки 2,4). Далее организован циклический процесс деления отрезка [ p, s ] пополам.

 

3.9.5. Метод Ньютона.

 

Метод Ньютона обладает более высокой скоростью сходимости по сравнению с другими методами При решении на ЭВМ уравнения вида F(y) = 0 также задают начальное приближение Ун и последовательно вычисляют следующие приближения. Расчет очередного приближения проводится по формуле

где — производная по .

После каждой итерации оценивают текущую погрешность рассмотренным выше способом. Начальное приближение в методе Ньютона целесообразно выбирать так, чтобы выполнялось условие

,

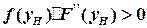иначе сходимость метода не гарантируется. Обычно выбирают или (и — границы отделения корней) в зависимости от того, в какой точке выполняется указанное выше условие.

3.9.6. Метод хорд.

 

В отличие от метода деления отрезка пополам в данном методе в качестве нового приближения к корню уравнения принимаются значения точек пересечения хорды (прямой, соединяющей ординаты у на концах интервала, внутри которого разыскивается корень уравнения) с осью абсцисс. Для точки пересечения хорды с осью абсцисс имеем

где и — концы интервала отделения корней. После вычисления по формуле (2.9) выполняется проверка текущей погрешности. Если |F()|<=Е_З, то полученное значение принимаем за корень уравнения, если же |F()|>Е_З, то выбираем тот из отрезков [а, ] или [,b], на концах которого функция F(y) имеет противоположные знаки, и снова определяем точку пересечения хорды с осью абсцисс с помощью соотношения (2.9).

 

3.9.7. Вычисление интегралов.

 

Существуют различные методы численного интегрирования : метод прямоугольников, метод трапеций, метод Симпсона и т.п. В основе этих методов лежит геометрическое толкование интеграла, согласно которому определенный интеграл

численно равен площади, ограниченной подынтегральной функцией , осью абсцисс и прямыми и . Для вычисления интеграла эту площадь разбивают на ряд элементарных полосок шириной h и заменяют каждую полоску более простой геометрической фигурой, для которой легко вычислить площадь. Значение интеграла получают путем суммирования площадей элементарных полосок.

При замене полоски на прямоугольник со сторонами и h получаем метод прямоугольников. Если полоску аппроксимировать трапецией с основаниями , и высотой h, то получим метод трапеций.

В общем случае геометрическая фигура аппроксимирует элементарную полоску приближенно, поэтому интеграл вычисляется с некоторой погрешностью E_T. При уменьшении ширины полоски h погрешность E_T уменьшается, однако это приводит к росту вычислительных затрат. Поэтому корректная постановка задачи численного расчета интеграла предполагает, что ширина элементарной полоски должна быть такой, чтобы результат получился с погрешностью, не хуже заданной при минимальных вычислительных затратах.

К сожалению нет точных математических формул для оценки текущей погрешности при расчете интеграла, поэтому воспользуемся алгоритмическим способом определения Е_Т .

Суть этого способа заключается в организации циклического процесса, в котором расчет интеграла проводится многократно для последовательно уменьшающихся значений шага h. Расчет проводят да тех пор, пока разность между очередным и предыдущим значениями интеграла не станет меньше заданного значения погрешности Е_З.

Рис.3.10.3

 

Укрупненная схема алгоритма, реализующего этот способ оценки погрешности, приведена на рис.3.10.3, где S1 — значение интеграла на предыдущем шаге расчета; S — значение интеграла на очередном шаге; k — количество точек деления интервала интегрирования; ER — признак ошибки; EPS — заданная погрешность; КМ — максимальное допустимое количество точек деления интервала интегрирования. Расчет начинается с К=2, S = 0; значение интеграла, полученное в блоке 3, присваивается переменной S. Если Е_Т= |S-S1| , больше заданной погрешности EPS, то полученное значение интеграла присваивается переменной S1 и количество точек деления интервала интегрирования увеличивается, например, в два раза. Расчет продолжается до тех пор, пока не выполнится условие в блоке 4 либо значение К не превысит заданное значение КМ. Величину КМ выбирают из разумных соображений так, чтобы при правильных данных алгоритм гарантировал определение значения интеграла с заданной погрешностью.

Контроль количества циклов в подобных задачах необходим, потому что:

1) цикл является итерационным и, следовательно, может потерять свойство конечности из-за ошибок в данных; 2) в каждом цикле шаг деления интервала интегрирования уменьшается в несколько раз, поэтому при больших К вычислительные затраты начинают катастрофически возрастать; 3) при очень малых h начинает играть роль погрешность округления, которая может стать больше заданной погрешности. В данном случае для контроля количества циклов используется признак Er. Если решение найдено менее чем за km циклов, то признак Er будет иметь значение 0. Значение Er=1 соответствует ситуации "Решение с заданной погрешностью не может быть найдено за km итераций".

Блок 3 на рис.3.10.3 — это циклический процесс суммирования площадей элементарных полосок. Число точек разбиения интервала интегрирования может быть большим, а подынтегральная функция — сложной, поэтому для построения эффективного алгоритма необходимо принимать меры по минимизации вычислительных затрат. Рассмотрим один из приемов построения эффективной расчетной формулы на примере метода трапеций.

Для метода трапеций расчетную формулу можно записать в виде

 

где n-номер шага по .

Нетрудно заметить, что в каждой точке по , кроме крайних, необходимо дважды вычислять значение подынтегральной функции. Раскроем скобки, сгруппируем подобные члены и запишем выражение для S в виде

 

В данном случае подынтегральная функция вычисляется в каждой точке только один раз.

Рис.3.10.4.

Схема алгоритма подпрограммы вычисления S приведена на рис.3.10.4. Вычисление подынтегральной функции оформлено в виде подпрограммы функции PF (с двумя параметрами K и X). Это повышает надежность программы, так как для расчета конкретного интеграла достаточно записать подынтегральную функцию только один раз – в подпрограмме PF.

 

3.10. Обработка двумерных массивов.

 

Массивы являются очень удобным средсвом для хранения и обработки больших групп логически связанных данных. Главным достоинством массивов является то, что они позволяют организовать обработку данных в виде компактных циклических процессов. Выше мы определили основные понятия связанные с массивами и рассмотрели примеры обработки одномерных массивов. Очень широкое распространение получили двумерные массивы. Это связано с тем, что независимо от способа хранения данных в памяти ЭВМ двумерный массив можно представить в виде плоской двумерной таблицы, состоящей из строк и столбцов. Например, двумерный массив У из шести элементов можно представить в виде таблицы, содержащей две строки и три столбца: У11 У12 У13

У21 У22 У23 .

Элемент двумерного массива также как и в случае одномерного обозначается индексированной переменной, которая имеет два индекса, например

У(К,М),

Где К – номер строки;

М – номер столбца.

При перемещении по строке изменяется второй индекс, а при смещении по столбцу изменяется первый индекс.

Основная причина использования двумерных массивов – высокая наглядность и возможность построения компактных циклических алгоритмов для обработки этих массивов.

Рис.3.10.5

 

Для решения задач связанных с обработкой двумерных массивов возможны 4 варианта:

- обработка по строкам;

- обработка по столбцам,

- цикл с предусловием;

- цикл с постусловием.

На рис.3.10.5 приведен общий вид алгоритма обработки двумерного массива по строкам и циклом с предусловием. Алгоритм представляет собой два циклических процесса, причем один цикл вложен в другой. Параметром внутреннего цикла является переменная m. Этот цикл обеспечивает обработку элементов строки (в процессе выполнения цикла изменяется второй индекс). Параметром внешнего цикла является переменная k. Этот цикл обеспечивает переход к очередной строке.

Пример. Составить фрагмент

Рис.3.10.6. алгоритма вычисления сумм элементов столбцов двумерного массива Z. Значения сумм элементов стобцов накапливать в одномерном массиве Sumst.Идея алгоритма.

Начиная с первого столбца суммируем элементы столбца и заносим полученное значение в одномерный массив. Затем переходим к следующему столбцу и снова суммируем.

Будем использовать следующие обозначения:

KS – количество столбцов; ST – количество строк;

K – счетчик строк; M – счетчик столбцов;

S – простая переменная для накопления суммы элементов столбца;

SUMST – одномерный массив для хранения сумм элементов столбцов.

Схема алгоритма решения этой задачи приведена на рис.3.10.6.