Энергетический метод исследования устойчивости.
 Основан на исследовании энергетических признаков устойчивого и не устойчивого равновесия упругой системы, согласно которым система находится в состоянии устойчивого равновесия, если её потенциальная энергия минимальна по сравнению с энергией смежных равновесных систем.
Основан на исследовании энергетических признаков устойчивого и не устойчивого равновесия упругой системы, согласно которым система находится в состоянии устойчивого равновесия, если её потенциальная энергия минимальна по сравнению с энергией смежных равновесных систем.
Если 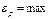 , то равновесие устойчиво.
, то равновесие устойчиво.
Пример: Определить Ркр для жёсткого стержня.
Выразим изменения упругой энергии системы через работу силы Р. Работа силы:
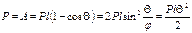
Работа совершаемая опорным моментом, определяется:
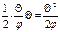
Изменение полной упругой энергии:

Энергетическим критерием потери устойчивости системы является условие:
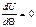

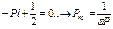
70 Учёт сил сопротивления при вынужденных колебаниях. Резонанс. Коэффициент динамичности.
При вынужденных колебаниях на систему кроме сил инерции и сил сопротивления действует сила P(t):
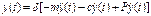



Общее решение уравнения:
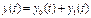
Где  - общее решение однородного уравнения;
- общее решение однородного уравнения;  - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения.
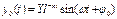
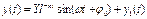
K- динамический коэффициент:
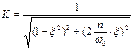
Где  - относительная частота.
- относительная частота.
При совпадении частот вынужденных колебаний 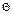 и частот собственных колебаний
и частот собственных колебаний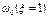 возникает резонанс и при n=0 динамический коэффициент стремится к бесконечности. Явление резонанса при действии периодических сил может привести к разрушению конструкции, поэтому при действии на конструкцию периодических сил с частотой
возникает резонанс и при n=0 динамический коэффициент стремится к бесконечности. Явление резонанса при действии периодических сил может привести к разрушению конструкции, поэтому при действии на конструкцию периодических сил с частотой 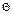 необходимо проверять, насколько близка эта частота к частоте свободных колебаний
необходимо проверять, насколько близка эта частота к частоте свободных колебаний  .
.
11. Применение уравнений 3-х моментов для расчёта неразрезных балок.
В качестве основной системы необходимо взять систему разрезных балок, полученную из заданной системы включением шарниров в опорные сечения. За неизвестное примем опорный изгиб. Моменты, очевидно, что число их равно числу промежуточных опор при наличии крайних шарнирных опор. Решение выбранной основной системы заключается в том, что эпюры моментов от единичных усилий распространяются в ней только на два соседних пролёта и значит, большое число побочных перемещений обращается в ноль. Для составления типового канонического уравнения в развёрнутом виде строим эпюры изгибающих моментов в основной системе от внешней нагрузки и единичных усилий. Из рассмотрения этих эпюр вытекает, что типовые канонические уравнения будет трёхчлен следующего вида:

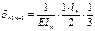
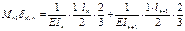

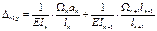
Подставляем: ……
 - площади эпюр моментов;
- площади эпюр моментов;
an , bn+1 – расстояние от центров тяжести этих эпюр. Умножим правую и левую части на 6EIc получаем:
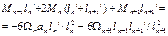

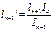
Уравнение 3-х моментов в общем виде. Если I=const
В уравнениях неизвестными являются 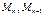 т.е. для расчёта неразрезной балки необходимо составить столько уравнений трёх моментов, сколько промежуточных опор, решая совместно внешним силам.
т.е. для расчёта неразрезной балки необходимо составить столько уравнений трёх моментов, сколько промежуточных опор, решая совместно внешним силам.
Если конец защемлён, для применения уравнения трёх моментов вводим дополнитьельный фиктивный пролёт. Для опоры ‘o’ составляем уравнения:

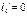
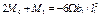
При отсутствии внешней нагрузки на крайнем 1-м пролёте у защемлённого конца: 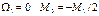
44,72. Решение системы ДУ с конечным числом степеней свободы. Вековое уравнение.
Рассмотрим балку несущую n сосредоточенных масс, совершающих свободные колебания в вертикальной плоскости.  Число степеней свободы = n. Х1, Х2, Х3 … Хn – силы инерции; у1, у2, у3 … уn – отклонение масс; А1, А2, А3 … Аn – амплитуды.
Число степеней свободы = n. Х1, Х2, Х3 … Хn – силы инерции; у1, у2, у3 … уn – отклонение масс; А1, А2, А3 … Аn – амплитуды.
Уравнения движения масс:

Сила инерции К – ой массы:


Подставим:

Разделим всё на 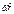 и обозначим
и обозначим 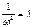 ;
;

Система уравнений будет выглядеть:
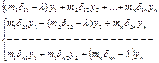
Эта система уравнений имеет не нулевое решение , если определитель составленный из коэффициентов при енизвестных у1…уn.
Вековое уравнение:
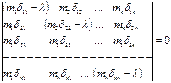
Раскрываем определитель и получаем полином степени n относительно 

Все корни этого уравнения положительны и у всех своя частота:
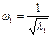 ;
; 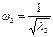 …
… 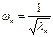 .
.
Совокупность частот – спектр.
Систему уравнений можно записать в математическом виде (вековое уравнение) 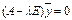 , где
, где
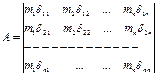 ;
;
Е – единичная матрица.
Решение с числом степеней свободы более 2 – 3 затруднительно.