Определение частоты свободных колебаний балки с распределенной массой при изгибе балки по произвольной кривой

В качестве примера с бесконечно большим числом степеней свободы рассмотрим балку с равномерно распределенной массой интенсивностью 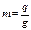 и постоянной жесткостью
и постоянной жесткостью 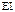 .
.
Спектр часто такой системы состоит из бесконечного множества частот, для определения которых будем исходить из дифференциального уравнения упругой линии балки, известного из курса сопротивления материалов:  (1), где M изгибающий момент в произвольном сечении балки, который на основании теоремы Д. И. Журавского может быть выражен через интенсивность инерционной нагрузки
(1), где M изгибающий момент в произвольном сечении балки, который на основании теоремы Д. И. Журавского может быть выражен через интенсивность инерционной нагрузки 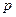 :
: 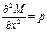 (2).
(2).
Обозначения частных производных приходится применять потому, что перемещение y является функцией двух переменных – координаты x и времени t.
Из выражений (1) и (2) следует: 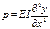 (3).
(3).
Вместе с тем интенсивность инерционной нагрузки балки может быть выражена через погонную массу m и через ускорение при колебаниях 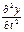 :
: 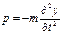 (4).
(4).
Приравнивая выражения (3) и (4) для нагрузки, получим дифференциальное уравнение свободных колебаний балки: 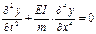 .
.
Это уравнение линейное, четвертого порядка, в частных производных.
Ограничимся отысканием только таких решений этого дифференциального уравнения, которые определяют стоячие волны, т. е. форму изгиба, не зависящую от времени.
При такой форме колебаний решение ДУ (4) может быть представлено в виде произведения двух функций, каждая из которых зависит от одного переменного: 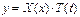 . Для нахождения функций X(x) и T(t) служат обыкновенные дифференциальные уравнения:
. Для нахождения функций X(x) и T(t) служат обыкновенные дифференциальные уравнения:
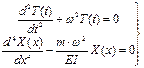 .
.
Эти дифференциальные уравнения имеют следующие решения:
 ;
; 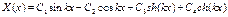 (5), где
(5), где 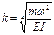 (6).
(6).
Значение k должно быть определено из условий на концах балки, которые зависят от способа закрепления этих концов. Всего для определения 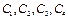 имеем 4 условия – по два на каждом конце.
имеем 4 условия – по два на каждом конце.
Так как рассматривается балка имеет шарнирные опоры, то прогибы и изгибающие моменты на опорах должны быть равны нулю, поэтому:
при  ,
,
при 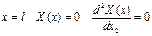 .
.
Из выражения (5) при этих условия определяем: 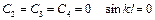 .
.
Но если 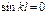 , то
, то 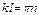 , где n произвольное целое число.
, где n произвольное целое число.
Следовательно 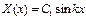 ,
, 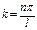 (7).
(7).
Приравнивая (6) и (7) получим выражение частот: 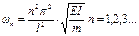
Таким образом, спектр частот действительно содержит их бесконечно множество. При этом частоты относятся друг к другу как квадраты целых чисел натурального ряда. Каждой частоте соответствует своя форма колебаний, т. е. своя форма стоячей волны.
Частоту основного тона свободных колебаний выражается такой формулой:
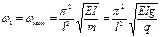 (8), где q=mg – интенсивность равномерной нагрузки на балку.
(8), где q=mg – интенсивность равномерной нагрузки на балку.
Для балки же с одной сосредоточенной силой Q посредине пролета частота свободных колебаний выражается такой формулой 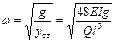 (9). Приравнивая выражения (8) и (9) найдем сосредоточенную силу
(9). Приравнивая выражения (8) и (9) найдем сосредоточенную силу 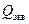 , эквивалентную равномерно распределенной нагрузке по частоте свободных колебаний балки
, эквивалентную равномерно распределенной нагрузке по частоте свободных колебаний балки 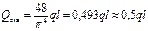 .
.
Таким образом, для нахождения частоты основного тона колебаний балки с равномерно распределенной нагрузкой можно заменить эту нагрузку половиной ее равнодействующей, приложенной посередине пролета.
37. Устойчивость арки кругового очертания под действием радиальной нагр-ки упруго защемленными пятами.
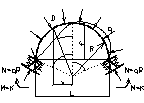


ДУ изгиба круговой арки 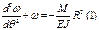

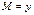

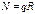
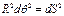
Изгибающий момент в произвольном сечении арки D. 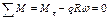
при потери устойчивости опоры поворачиваются на какой-то угол
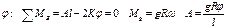
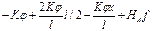
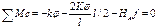
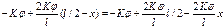

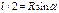
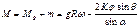
уравнение при потери устойчивости 
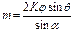

Общее решение: 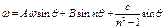 Найдем А,В и С. С – зависит от угла поворота
Найдем А,В и С. С – зависит от угла поворота 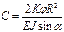 . Граничные условия
. Граничные условия 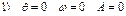
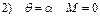
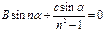
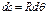
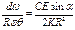
сократим на R: 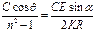
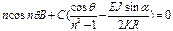
1. A=B=C=0  При
При 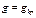 потери устойчивости не произошло, но невозможно найти
потери устойчивости не произошло, но невозможно найти 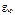
2. 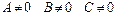 Составляем определитель из коэф-ов кот-е прирав-ся к 0
Составляем определитель из коэф-ов кот-е прирав-ся к 0

Раскрываем: 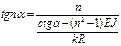
Решаем путем подбора 
