рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Государство
- /
- Вид работы: Лекции
- /
- Предел числовой последовательности.
Реферат Курсовая Конспект
Предел числовой последовательности.
Предел числовой последовательности. - Лекция, раздел Государство, Лекция 5. Числовая последовательность и её предел Определение 1: Число А Называется Пределом...
Определение 1: Число а называется пределом числовой последовательностью {хn}, если для любого положительного числа e существует номер N такой, что при всех n>N выполняется неравенство |xn-a|<e. Последовательность {хn} – называется сходящейся. 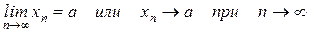 .
.
Теорема 1: Сходящаяся последовательность имеет только один предел.
Определение 2: Последовательность {хn} не являющаяся сходящейся называется расходящейся.
Из определения 1 предела следует, что каким бы малым мы ни взяли число e>0, начиная с некоторого номера N все элементы последовательности будут отличаться от числа а меньше, чем на e, то есть элементы последовательности неограниченно приближаются к числу а при неограниченном возрастании номера n.
Определение 3: Число а не является пределом числовой последовательности {хn}, если существует положительное число e, что для любого номера N найдётся номер n>N такой, что выполняется неравенство |xn-a|³e.
Из |xn-a|<e Þ -e<xn-a<e Þ а-e<xn<а+e, то есть элемент xn находится в e-окрестности точки а.
Следствие 1: Пусть {хn} сходится и имеет своим пределом некоторое число а.
Тогда разность {хn-а}={an} является бесконечно малой последовательностью, так как для любого e>0 существует номер N такой, что при всех n>N выполняется неравенство |xn-a|=|an|<e.
Следствие 2: Всякая бесконечно малая последовательность является сходящейся и имеет своим пределом 0.
Следствие 3: Любой элемент xn сходящейся последовательности, имеющей пределом число а можно представить в виде: xn=а+an, где an элемент бесконечно малой последовательности {an}. Справедливо и обратное.
Определение 4: Число а называется пределом числовой последовательностью {хn}, если для любой e-окрестности точки а существует номер N такой, что все элементы xn с номерами n>N находятся в этой e-окрестности.
Бесконечно большие последовательности имеют бесконечный предел 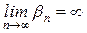
– Конец работы –
Эта тема принадлежит разделу:
Лекция 5. Числовая последовательность и её предел
Лекция Числовая последовательность и е предел Числовая...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Предел числовой последовательности.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов