Решение дифференциальных уравнений в частных производных

Ключевые слова: частная производная; уравнения в частных производных: эллиптического, параболического, гиперболического типа; квазилинейное уравнение; метод сеток решения дифференциальных уравнений [6,7,9].

Решение дифференциальных уравнений в частных производных имеет большое прикладное значение. Формализация и построение математических моделей различных явлений и процессов в физике, электротехнике, электронике, механике и т.п. часто приводит к дифференциальным уравнениям, выражающим соотношения между изменениями физических величин. При этом решение уравнений должно находиться в заданном интервале или области и удовлетворять некоторым дополнительным условиям – начальным и граничным (краевым). Получаемое решение должно быть устойчивым относительно малых изменений начальных и граничных условий. В этом случае задача считается корректно поставленной.

Общий вид дифференциального уравнения в частных производных для двух независимых переменных второго порядка можно представить формулой

 

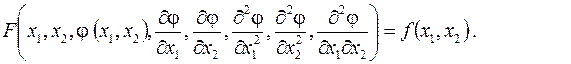
Квазилинейное уравнение второго порядка с двумя независимыми переменными имеет вид

,

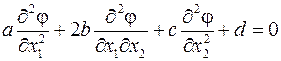где φ( x₁, x₂ ) – искомая функция; a,b,c,d – функции от 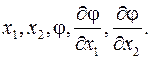Тип данного уравнения определяется соотношением коэффициентов a,b,c

1. ac − b² < 0 для гиперболического типа;

2. ac − b² = 0 для параболического типа;

3. ac − b² > 0 для эллиптического типа.

Если в рассматриваемой области дискриминант ac − b² меняет знак, то уравнения относят к смешанному типу.

Определение типа уравнения необходимо для определения состава исходной информации:

– для гиперболического типа задаются краевые условия и начальные условия для φ и ;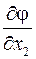

– для параболического типа задаются краевые условия и начальные условия для φ;

– для эллиптического типа задаются только краевые условия.