Структура простого категорического силлогизма

В традиционной логике простым категорическим силлогизмом называется любое умозаключение, в котором в качестве посылок выступают два категорических суждения. Заключением в нем является (категорическое) суждение, в котором содержатся понятия (термины), каждое из которых встречается только в одной посылке. В каждой из посылок имеется еще одно одинаковое для них понятие (термин), которое отсутствует в заключении.

Понятие, общее для обеих посылок, называется средним термином (terminus medius). Понятие, выступающее в роли предиката заключения, именуют большим термином; понятие, которое выполняет роль субъекта заключения, называют меньшим термином. Больший и меньший термины называют крайними. Больший термин (Р) содержит большая посылка, меньший термин (S) содержит меньшая посылка. В стандартно построенном силлогизме большая посылка должна стоять первой.

В умозаключении

(I) 1. Все млекопитающие (М) – теплокровные (Р)

2. Все тюлени (S) - млекопитающие (М)

3. Все тюлени (S) - теплокровные (Р)

являющимся примером простого категорического силлогизма, понятие «тюлени» - субъект (S) заключения (меньший термин), «теплокровный» - его предикат (Р) (больший термин), «млекопитающие» - средний термин (М), большая посылка – первая, меньшая – вторая.

Силлогистика (учение о силлогизмах) описывает схемы умозаключений, которыми можно пользоваться как правилами вывода. Пример схемы простого силлогизма:

МаР

(II) SаМ

SаР

Данная запись является схемой вышеприведенного силлогизма (I).

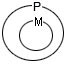
Переход от посылок к заключению в силлогизме связан с ролью среднего термина: отношение субъекта S и предиката Р в заключении устанавливается в зависимости от их отношения к среднему термину М. Рассмотрим для примера схему (II). Здесь первая посылка содержит утверждение о том, что все предметы множества М включаются во множество Р. В свою очередь, вторая посылка указывает, что все предметы множества S включаются во множество М. Графически эти соотношения могут быть представлены так:

1. МаР:	2. SаМ:

Теперь совместим эти схемы:

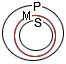
На этой схеме хорошо видно, что все предметы множества S оказываются также элементами множества Р, а именно это обстоятельство констатируется в заключении SаР рассматриваемой схемы.