Интуитивистская альтернатива

 

Все беды обоснования интуиционизм видит не собственно в логике (в несовершенстве ее аппарата), а в самой математике и именно в неточном использовании ее понятий, прежде всего – понятия бесконечности. Первично математическое мышление, а язык и логика суть несовершенные способы его выражения.

Достичь точности и должна помочь интуиция. Необходимо, чтобы все построения опирались только на те утверждения, которые санкционированы изначальной интуицией. Не вдаваясь пока в анализ философских аспектов этого понятия, отметим следующее. Материал, из которого созидаются математические объекты, не является собственно математическим. Это актуально переживаемое. Оно очищено от всего, берется лишь сам акт восприятия, так называемые «жизненные моменты», непосредственно воспринимаемые субъектом. Изначальная интуиция – деятельность, связанная с глубинным ощущением времени. Идея выводить число на основе времени восходит еще к Канту. Человеку всегда дано нечто переживаемое. В качестве элементарного акта мысленных построений интуиционизм рассматривает разделение моментов жизни на качественно различные части, которые, будучи разъединены лишь временем, могут быть снова объединены. В силу сменяемости и последовательности событий мы, воспринимая некоторый объект, можем говорить о следующем за ним объекте. Одновременно происходит очищение разделения переживаемого от какого бы то ни было эмоционального содержания до момента, пока не останется интуиция абстрактного двуединства. «Два в одном» – это и есть базисная интуиция Я. Брауэра.

Так переживаемое во времени t как «настоящее 1» в силу течения времени и возможности удерживать памятью прошлое в нашем сознании двоится на прошлое и настоящее. В итоге имеем: «прошлое – 1, настоящее – 2». Последнее в следующий момент времени (fe) также двоится на настоящее и прошлое, в результате получаем «прошлое – 2, настоящее – 3». При том они даны как очищенные от любого конкретного содержания элементов деления. Складывается числовой ряд:

t₁ настоящее 1;

t₂ прошлое 1 – настоящее 2;

t₃ прошлое 2 – настоящее 3 и т. д.

 

Характеризуя механизм математического построения числа, А. Гейтинг писал: «В построении любого предмета мы представляем его себе как сущность, отвлекаясь от его частных свойств. Мы познаем также возможность неограниченного повторения этой сущности. Здесь-то и лежит источник понятия натурального числа» ¹.

Отметим, что к аналогичному представлению подошел известный немецкий ученый Г. Гельмгольц, предвосхитив интуиционистское понимание происхождения чисел. Пытаясь выявить психологические источники аксиом арифметики, он писал: «Счет есть операция, основывающаяся на том, что мы находимся в состоянии удерживать в памяти последовательность, в которой являлись во времени один за другим акты нашего сознания»².

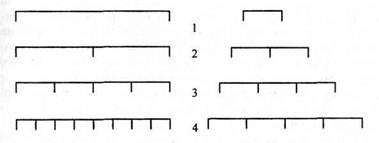
Стоит особо подчеркнуть тот факт, что хотя по внешним описаниям рассуждения интуиционистов по поводу возникновения числового ряда кажутся построенными на механическом повторе восприятия, на самом деле они, вводя интуицию, пытались уйти от автоматизма, скорее характерного для строго логического мышления и сторонников логицизма. Математическая традиция, на которую опирались логицисты, исповедовала математику «чистых количеств», она и стала опорой математического естествознания. Интуиционизм же нащупывал выход к другим основаниям, в истоках которых находится, как выражались иные, «математика качеств». Она связана не со сложением (механическим повторением), а с операцией деления, когда «два» является не внешним повторением «одного», а внутренним результатом его саморасщепления. Подобное раздвоение единого таит начала бесконечного числа. Это хорошо иллюстрирует схема Эрнста Бинделя.

 

 

 

¹ Гейтин А Интуиционизм. М.: Мир, 1965. С. 22.

² Гельмгольц Г. Счет и измерение. Казань, 1898. С. 6.

 

 

В ряду справа – операции механического мышления и+1, в столбце слева – акты человеческого мышления 1 : п.

Если правый ряд отрицает левый, то левый органически содержит в себе правый как один из моментов анализа.

Итак, первичные математические объекты постулируются на основе интуиции.

Другим важным пунктом интуиционистской программы был пересмотр принципов конструирования систем математических объектов. Я. Брауэр полагал, что они должны формироваться на базе некоторых принципов построения, но не вводиться в математический обиход с самого начала целиком, как множества, отвечающие требованиям заданных аксиом.

Все это существенно меняло подход к обоснованию математики. Для логицизма математический объект существует, если его определение не приводит к противоречию. С точки же зрения интуиционизма существование объекта оправданно, если он задан эффективным определением, указывающим способ (алгоритм) построения. Наиболее адекватно отвечают этому генетические, фиксирующие происхождение объекта определения. Так, согласно родовидовому определению (ближайший класс и отличительные признаки данного подкласса), окружность – замкнутая кривая, все точки которой расположены на одинаковом расстоянии от центра. В соответствии с генетическим определением окружность есть замкнутая кривая, полученная движением точки b отрезка ab вокруг неподвижной точки a.

Разъясняя смысл интуиционистского подхода, Вейль пишет: «Для математика совершенно безразлично, что такое окружность, для него принципиально знать, каким образом может быть задана окружность...» То есть не суть важно, что собой представляет окружность, каково ее математическое содержание, имеет значение лишь способ, каким она может быть построена. Точно так же никто не может определить, что такое функция. Однако функция задана, «если каждому вещественному числу a каким-либо определенным закономерным образом ставится в соответствие число b (например, при помощи формулы b=2a+1). Тогда говорят, что b является значением функции f при значении аргумента, равном а» .

По идее логицистов, все производные понятия дедуцируются из исходных, здесь же понятия рассматриваются не как выводимые, а

__________

¹ Вейль Г. О философии математики. М; Л.: ГТТИ, 1934. С. 39.

 

как порождаемые в некотором определенном порядке. Налицо генетический (вместо аксиоматического) метод построения теории, вместо дедукции – конструкция¹.

Соответственно в аксиоматике исходным является система высказываний, описывающая некоторую область объектов, и система логических действий над ними. Важны отношения, устанавливаемые между объектами, тогда как последние могут обладать любой природой (получать самую различную интерпретацию). При генетическом же построении исходными являются не высказывания, а наличные, данные объекты, которые вводятся остенсивно, то есть путем прямого указания на объект, и уточняются индуктивными определениями. Процедура построения задается таким образом: (1) указываются исходные объекты, которые суть объекты теории; (2) утверждается, что результаты применения определенных операций к (1) есть также объекты теории; (3) утверждается, что объекты, полученные в результате осуществления пунктов (1) и (2), – единственные объекты теории. Например, (1) 1 есть число; (2) если а есть число, то а 1 – число; (3) ничто другое не есть число².

В свете новых идей пересматриваются интуиционизмом и логические принципы.

Абстракция потенциальной (не актуальной) осуществимости предполагает, что элементы бесконечного множества не могут быть заданы одновременно, они последовательно возникают в процессе его построения. Это становящаяся бесконечность, не имеющая последнего члена, ибо после n-шагов всегда можно сделать (n+1)-й шаг. Так, вместо актуальной бесконечности принимаемой логицизмом и традиционной математикой, вводится понятие потенциальной бесконечности.

Ультраинтуиционистское течение (одним из представителей которого является выдворенный в свое время из СССР сын поэта Сергея Есенина А. Есенин-Вольпин), отказывается не только от актуальной, но и от потенциальной бесконечности, признавая лишь конечные множества, – концепция «откровенной точки зрения». В соответствии с этим подвергаются уточнению понятия всеобщно-

______________

¹ Следует заметить, что интуиционистские теории так же могут быть изложены аксиоматически (и это сильнейший аргумент в пользу интуиционизма), однако здесь используются другие методы.

² Подробнее см.: Смирнов В.А. Генетический метод построения научной теории // Философские вопросы современной формальной логики. М: Изд-во АН СССР, 1962. С. 263-285.

 

ста и квантора общности. Математические высказывания, содержащие выражения «все», «каждый» и т. п., принимаются, только если указан способ их получения. В частности, нельзя говорить обо всех, но о каждом можно.

Особое внимание уделяется закону исключенного третьего. Утверждается, что принципы классической логики не имеют абсолютной приложимости, не зависящей от содержания предмета обсуждения. В частности, закон исключенного третьего, сохраняя силу для конечных множеств, утрачивает ее в области потенциально бесконечного как незавершенного бесконечного.

Рассмотрим предикат Р(х), где областью изменения переменной является множество М Согласно закону исключенного третьего, либо в М имеется х, такой, что Р(х), либо такого х, что Р(х), нет.

Символически $х Р(х) Ú $х Р(х). Если М – конечное множество, и предикат Р(х) таков, что мы можем установить для каждого х, истинно или нет Р(х), закон исключенного третьего действителен. В случае же, когда М – бесконечное множество, у нас нет гарантии, что мы найдем такой х в некоторое конечное число операций. Поскольку же необходим полный перебор значений х, а эта процедура бесконечна, то мы так и не получим ответа на интересующий нас вопрос, ибо такого х, что Р(х), может, в М вообще не быть либо он расположен слишком далеко. По шутливому замечанию Г. Вейля, закон исключенного третьего действителен лишь для Господа Бога, обозревающего мир в целом.

В связи с этим интуиционизм не приемлет и метода доказательства от противного, поскольку оно покоится на законе исключенного третьего. Согласно интуиционизму, принятие $х Р(х) на том основании, что принятие $хР(х)ведет к противоречию, не правомочно. Из этого доказательства следует лишь $х Р(х), то есть неверно, что не существует такой х, что Р(х).

Критические выступления против классической логики заставили интуиционистов разработать новые, уточненные принципы логики. Первое интуиционистское исчисление построил Гейтинг в 1930 г. Для самих интуиционистов исчисление не представляло интереса, зато другие математики получили, наконец, возможность познакомиться с новой логической системой. Тут же были предприняты попытки ее анализа. Первым, кто получил результаты, стал отечественный математик А.Н. Колмогоров, который показал,

 

что гейтинговское исчисление поддается интерпретации в терминах классической логики как исчисление проблем (задач). При этом, оставляя понятия «проблема» и ее «решение» неопределенными (как это и делается обычно), интуиционизм ставит в соответствие конъюнкции решение двух проблем, дизъюнкции – хотя бы одной из двух, импликации – сведение решения одной проблемы к решению другой. Интуиционистская логика оказывается здесь частью классической. Вместе с тем есть и другие интерпретации, где, наоборот, классическая логика переводима в интуиционистскую.