Основные законы алгебры логики

Способ определения истинности сложного выражения путём построения таблиц истинности становится громоздким при возрастании количества логических переменных, так как число наборов резко увеличивается.В таких случаях используют способы упрощения формул путём применения равносильных преобразований. Ниже в таблице приведены основные законы алгебры логики.

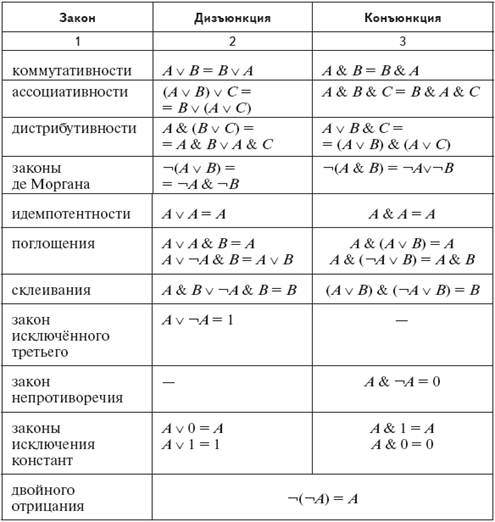
Выполняется закон двойственности: если конъюнкцию заменить дизъюнкцией, дизъюнкцию заменить конъюнкцией, 0 заменить на 1, а 1 на 0, то равносильность, записанная для дизъюнкции, перейдёт в равносильность, записанную для конъюнкции.

Под упрощением формулы понимают равносильное преобразование,приводящее к нормальной форме.

Выражение имеет нормальную форму, если в нём используются только операции дизъюнкции, конъюнкции и отрицания переменных. При этом не используются двойное отрицание и отрицание выражений.

Для приведения выражения к нормальной форме в первую очередь избавляются от отрицаний выражений, операций импликации, эквиваленции и исключающего или. Затем используют законы алгебры логики для уменьшения количества вхождений переменных.

Применение законов алгебры логики, похожих на законы преобразований в обычной алгебре, не вызывает затруднений. Рассмотрим примеры применения законов склеивания, поглощения, идемпотентности, законов де Моргана, не имеющих аналогов в обычной алгебре.

Закон склеивания А & В ∨ ¬А & В = В и (А ∨ В) & (¬А ∨ В) = В.

1. Упростить выражение X & Y & Z ∨ ¬X & Y & Z. В выражении X & Y & Z ∨ ¬X & Y & Z переменной А соответствует переменная X, переменной В соответствует выражение Y & Z. Тогда в результате упрощения получим

2. Упростить выражение (X ∨ Y ∨ Z) & (X ∨ ¬Y ∨ Z). В выражении (X ∨ Y ∨ Z) & (X ∨ ¬Y ∨ Z) переменной А соответствует переменная Y, переменной В соответствует выражение X ∨ Z. Получим

3. Упростить выражение X & Y & Z ∨ ¬X & Y & Z ∨ X & ¬Y & Z ∨ ∨ X & Y & ¬Z. В этом примере, на первый взгляд, закон склеивания можно использовать только один раз — для первого слагаемого и одного из трёх других: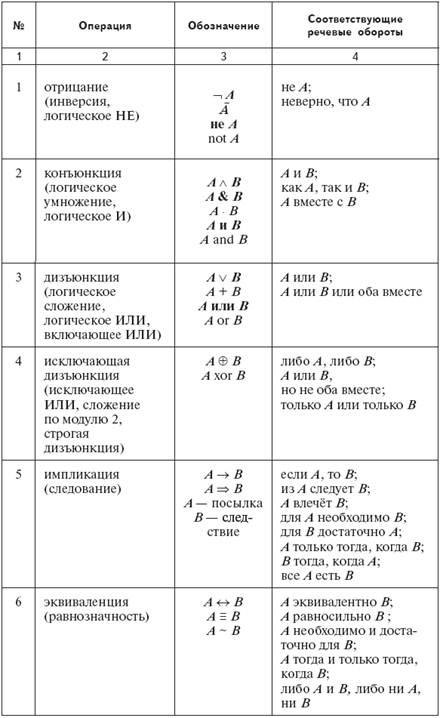

Но если использовать закон идемпотентности А = А ∨ А, можно в исходную формулу добавить ещё два слагаемых, совпадающих с первым. Получим

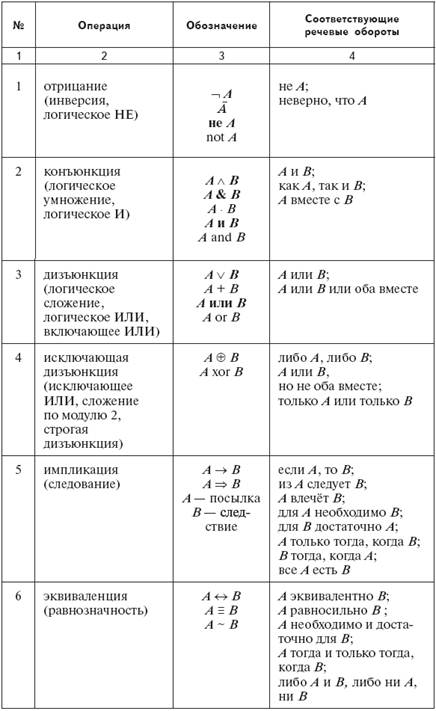
Закон поглощения (см. табл.

)

1. Упростить выражение X ∨ X & Y ∨ X & Z ∨ X & Y & Z. Для всех слагаемых общим сомножителем является X. Последовательно применяя закон поглощения А ∨ А & В = А, получим

2. Упростить выражение X ∨ ¬X & Y ∨ ¬X & Z ∨ ¬X & Y & Z. Последовательно применяя закон поглощения А ∨ ¬А & В = А ∨ В, получим

В предпоследней строке к выражению Z ∨ ¬X & Y & Z был применён закон поглощения А ∨ А & В = А.

Упростить выражение (X ∨ Y) & (X ∨ Y ∨ Z) & (X ∨ Y ∨ ¬Z). Для всех сомножителей общим слагаемым является X ∨ Y, это и есть результат упрощения.

Совет: В операциях конъюнкции и дизъюнкции имена переменных записывайте в алфавитном порядке, причём сначала переменную,а затем её отрицание.