Обработка "плохих" данных

Если в результате эксперимента все же получены данные с мультиколлинеарностью, то можно попытаться получить приемлемую по статистическим качествам модель посредством специальных способов обработки данных.

Прежде сего в таких случаях рекомендуется применять методы решения системы нормальных уравнений т.н. устойчивыми методами.

Как известно, результаты эксперимента записываются в расширенную матрицу наблюдений:

№ опыта	х₁	х₂	...	х_n	y
	f₁₁	f₂₁	...	f_n1
	f₁₂	f₂₂	...	f_n2
:	...	...	...	...
N	f_1N	f_2N	...	f_nN

В этой матрице вместо значений факторов могут стоять базисные функции f_j, если нелинейная зависимость описывается линейной по параметрам моделью. Для получения коэффициентов регрессии МНК матрица наблюдений записывается в виде системы линейных уравнений, которая в матричной форме имеет вид:

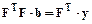
(10.1)

где F – матрица регрессоров (7.2);

b – вектор искомых коэффициентов регрессии;

у – вектор откликов:

Произведение транспонированной матрицы регрессоров на ее значение F^TF = Gназывается информационной матрицей МНК. Как уже известно, при наличии мультиколлинеарности решение системы (10.1) обычными методами, в частности, методом Гаусса, является неустойчивым – добавление или изъятие небольшого количества данных приводит к резкому изменению величины коэффициентов регрессии и к большим ошибкам при их оценивании. Менее чувствительными к мультиколлинеарности являются методы треугольного разложения и ортогонального разложения.

При решении системы уравнений МНК методом треугольного разложения обычно применяется один из вариантов этого метода, использующий т.н. разложение Холесского. Этот метод применим только к симметричным положительно определенным матрицам. Исходная информационная матрица G представляется в виде G= L·L^-1, где L – нижняя треугольная матрица (т.е. матрица, у которой по верхнюю сторону от диагонали находятся нули). Например:

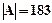
После этого задача сводится к решению двух простых систем линейных уравнений:

где С – вспомогательный вектор;

Z – вектор, элементами которого являются суммы произведений:

Метод ортогонального разложения (QR – разложение) не предъявляет к матрице G столь жестких требований. Единственное требование – матрица G должна быть не вырожденной, т.е. ее определитель должен быть отличен от нуля. По этому методу информационная матрица представляется в виде: G = QR, где Q - ортогональная матрица (т.е. состоящая из ортогональных друг другу единичных векторов), а R – верхняя треугольная матрица с неотрицательными диагональными элементами. Например:

Решение системы нормальных уравнений сводится к решению системы:

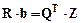Разложения Холесского и QR – разложение весьма просто выполняются в MathCAD встроенными специальными функциями. Решение матричных уравнений выполняется специальными программами.

По вычислительной устойчивости на первом месте метод ортогонального разложения, далее идет метод треугольного разложения и на последнем месте – метод Гаусса. Однако при сильной мультиколлинеарности ни один из этих методов не гарантирует получения достаточно точных оценок коэффициентов регрессии. Поэтому разработаны и применяются методы предварительного центрирования переменных и метод регуляризации.