Точная верхняя (нижняя) граница
Совокупность всех верхних границ Е обозначается через Еs, всех нижних границ - через Еi. В случае, когда Еs (Еi) непусто, говорят, что Е ограничено сверху {снизу). Если элемент z принадлежит пересечению  (соответственно,
(соответственно, 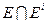 ), то он является наибольшим {наименьшим} элементом множества Е. Выражение типа (Еs)i эквивалентно Еsi. Непустота пересечения
), то он является наибольшим {наименьшим} элементом множества Е. Выражение типа (Еs)i эквивалентно Еsi. Непустота пересечения  {
{ } означает, что среди верхних (нижних) границ Е имеется наименьшая (наибольшая); ее называют точной верхней {нижней) границей, или верхней {нижней) гранью множества Е.
} означает, что среди верхних (нижних) границ Е имеется наименьшая (наибольшая); ее называют точной верхней {нижней) границей, или верхней {нижней) гранью множества Е.
Утверждение. Пересечения  {
{ } не могут содержать более одного элемента
} не могут содержать более одного элемента
Доказательство.
Пусть . Тогда х ≤ у, поскольку
. Тогда х ≤ у, поскольку
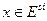 . Аналогичным образом убеждаемся в справедливости противоположного неравенства y ≤ x А тогда х = у.
. Аналогичным образом убеждаемся в справедливости противоположного неравенства y ≤ x А тогда х = у.
Верхняя (нижняя) грань, если она существует, обязательно единственна. Точная верхняя граница (supremum) множества Е обозначается символом sup Е, точная нижняя граница (infimum) — символом inf Е.
Если элементы Е занумерованы с помощью некоторого множества индексов Ξ = {ξ}, то применяются обозначения
sup Е = 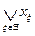 inf Е =
inf Е = 
Если Е состоит из конечного числа элементов х1,х2,, ..., хn, то пишут
sup Е = 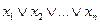 или sup Е =
или sup Е = 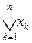
inf Е=  или inf Е=
или inf Е= 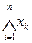 .
.
Основные свойства верхних и нижних границ в произвольном частично упорядоченном множестве X.
1. Если 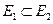 то
то 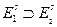 ,
, 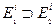 .
.
2. Если 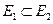 и существуют sup Е1, и sup Е2 (inf Е1 и inf Е2 ), то
и существуют sup Е1, и sup Е2 (inf Е1 и inf Е2 ), то
sup Е1 ≤ sup Е2 inf Е1 ≥ inf Е2
3.Соотношения х ≤ у, 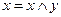 ,
, 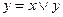 равносильны.
равносильны.
4. Пусть E = {Е}—непустой класс подмножеств X, каждое из которых имеет верхнюю {нижнюю) грань. Предположим далее, что совокупность этих граней в свою очередь имеет supremum (соответственно infimum). Тогда этот последний представляет собой верхнюю (нижнюю) грань объединения  .
.
Это свойство называется свойством ассоциативности граней. Его можно выразить формулами
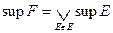 и
и 
предполагая, что фигурирующие в правых частях грани существуют.
Свойства 1-3 очевидны.
Остановимся на доказательстве ассоциативности, ограничившись, случаем верхних граней. Обозначим
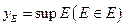 ,
, 
Для произвольного элемента  можно указать множество
можно указать множество  , которому он принадлежит. Поэтому
, которому он принадлежит. Поэтому 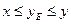 ,
,  Теперь, взяв произвольно
Теперь, взяв произвольно 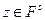 , замечаем, что в силу 1будет
, замечаем, что в силу 1будет 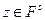 для каждого
для каждого  , то есть
, то есть 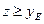 Видим, что элемент я есть верхняя граница для множества всех
Видим, что элемент я есть верхняя граница для множества всех 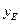 , и поэтому
, и поэтому  . Доказали, что элемент y есть наименьшая из верхних границ множестваF, то есть точная верхняя граница.
. Доказали, что элемент y есть наименьшая из верхних границ множестваF, то есть точная верхняя граница.
Cвойства, связанные с преобразованием границ при изоморфизмах и дуальных изоморфизмах.
5. Если φ - изоморфизм, то всегда
 ,
,
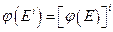 .
.
6. Если φ - изоморфизм, то всегда
 ,
,
 .
.
при условии, что хотя бы одна из граней, фигурирующих в равенстве, существует.
7. Если φ - дуальный изоморфизм, то всегда
 ,
,
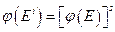 .
.
8. Если φ - дуальный изоморфизм то всегда
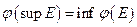 ,
,
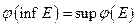 .
.
с той же оговоркой, что и в 6.
Отметим в заключение очевидную изотонность операций  и
и  .
.