Структура
Частично упорядоченное множество X называется структурой, если в нем любое двухэлементное множество 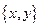 имеет точные границы
имеет точные границы 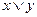 и
и 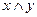 .
.
Лемма 1. В любой структуре всякое конечное множество элементов имеет точные границы.
Упражнения
1.Упростить выражение 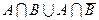
2. Докажите, что следующие условия эквивалентны 1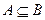 , 2.
, 2.  , 3
, 3 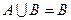 , 4
, 4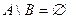 , 5
, 5  .
.
3. Записать множество  через пересечение (
через пересечение (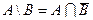 ).
).
4. Докажите, что  . Как называется этот закон?
. Как называется этот закон?
5. Докажите, что  . Как называется этот закон?
. Как называется этот закон?
1. Группа студентов насчитывает 25 человек. Из них 15 любят математику, 10 — физику, 8 — не любят ни математику, ни физику. Сколько студентов любят и математику, и физику?
2. На собрании студентов-отличников были как студенты второго курса, так и студенты третьего курса. Все они либо любители прозы, либо любители поэзии. Студентов-юношей было 16, а любителей прозы — 24. Студентов-девушек было ровно столько, сколько юношей любителей прозы. Сколько студентов было на собрании?
3. В группе из 100 студентов английским языком владеют 28 человек, немецким — 30, французским — 42, английским и немецким — 8, английским и французским— 10, немецким и французским— 5, а всеми тремя языками владеют 3 студента. Сколько студентов не знают ни одного из названых языков?
Комментарий
ОТСТУПЛЕНИЕ
Существование и анализ парадоксов в теории множеств способствовали развитию так называемого конструктивизма — направления в математике, в рамках которого рассматриваются только такие объекты, для которых известны процедуры (алгоритмы) их порождения. В конструктивной математике исключаются из рассмотрения те понятия и методы классической математики, которые не заданы алгоритмически
Первым и важнейшим математическим пространством является трехмерное эвклидово пространство, предоставляющее собой приближенный абстрактный образ реального пространства. Общее понятие пространства в математике сложилось в результате обобщений и изменений понятий геометрии эвклидова пространства.
В современной математике пространство — это множество объектов, называемых точками, введенными отношениями между точками и теми или иными операциями над элементами множеств.
Примерами пространств могут служитьметрическое пространство, нормированное пространство, пространство событий, пространство состояний и целый ряд других пространств.Метрическое пространство — это множество точек Х с расстоянием между ними d>0, удовлетворяющем трем аксиомам:
1) d(х, у) =0 тогда и только тогда, когда х=у (аксиома идентичности);
2) d(х, у) = d(у, х) (аксиома симметрии);
3) d(х, у) = d(х, z) + d(y,z) + d(y,z), гдех,у,z Х (аксиома треугольника).
Х (аксиома треугольника).
Расстояние d(х, у) называетсяметрикой, а пара (х, d) —метрическим пространством. Простейшим примером метрического пространства является множество действительных чисел Х с расстоянием между ними d = х - у.
В двумерном эвклидовом пространстве Е2(плоскости) расстояние между двумя точками М1(х1,y1), М2(х2 ,у2) определяется по выражению d2 = (х1 – х2)2 + (у1 – y2)2. Эта же формула распространяется на трехмерное эвклидово пространство d2 = (х1 – х2)2 + (у1 – y2)2+ (z1 - z2)2 и на многомерное его обобщение Еn, в котором элементами множества Х являются упорядоченные наборы <х1, х2, ..., хi ..., хn> действительных чисел: расстояние между двумя точками этого пространства определяется по выражению
d2 = (х1 – х2)2 + (у1 – y2)2 + (z1 - z2)2
Линейные пространства — это такие множества, элементы которых удовлетворяют следующим условиям:
1) для каждой пары элементов х,у Х определен третий элемента z
Х определен третий элемента z Х, называемый их суммой и обозначаемой как х+у. При этой сумма удовлетворяет следующим условиям: х+у=у+х,
Х, называемый их суммой и обозначаемой как х+у. При этой сумма удовлетворяет следующим условиям: х+у=у+х,
x+(у+v) = (x+у)+v;
2) во множестве Хсуществует такой элемент 0, что х+0 = х для всех х X;
X;
3) для всех х Х существует такой элемент-х, что х+(-х) = 0;
Х существует такой элемент-х, что х+(-х) = 0;
4) для любого числа а и любого элемента х X определен элемент а такой, что (а+β)х = ах+βx, а(х+у) = ах + ау.
X определен элемент а такой, что (а+β)х = ах+βx, а(х+у) = ах + ау.
Очевидным примером линейного пространства является множество действительных чисел с обычными правилами их сложениям умножения. Если n-мерном эвклидовом пространстве E* упорядоченные наборы чисел <х1, ..., хi, ..., хn> Х считать координатами векторов с условием, что нулевой вектор – это вектор с нулевыми значениями <х1, ..., хi, ..., хn>, то такое векторное пространство линейное, потому что операции действия с вектором отвечают перечисленным выше аксиомам.
Х считать координатами векторов с условием, что нулевой вектор – это вектор с нулевыми значениями <х1, ..., хi, ..., хn>, то такое векторное пространство линейное, потому что операции действия с вектором отвечают перечисленным выше аксиомам.
Дальнейшим расширением понятия линейного пространства является линейное нормированное пространство. Это такое пространство, в котором для каждого элемента х X существует неотрицательное число ||х||, называемое его нормой и удовлетворяющее следующим условиям:
X существует неотрицательное число ||х||, называемое его нормой и удовлетворяющее следующим условиям:
||х|| = 0, тогда и только тогда, когда х = 0;
||ах|| = а||х||, где а — некоторое число;
||х+y|| ≤ ||х|| + ||y||
Линейное нормированное пространство является метрическим пространством с нормой d = ||х - y||, так как эта норма удовлетворяет аксиомам метрического пространства:
||х - y|| = 0, если х = у; ||х - y|| = ||y-х||; ||х - y|| ≤ ||х - z|| + ||z - y||
Нормой ||х|| в одномерном векторном пространстве Е1является абсолютная величина х. Нормой двумерного пространства (плоскости) Е2 является длина вектора, вычисляемая по выражению ||х|| = 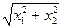 . Для n-мерного векторного пространства норма ||х|| определяется по аналогии с двухмерным пространством
. Для n-мерного векторного пространства норма ||х|| определяется по аналогии с двухмерным пространством
||х|| = 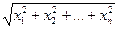 .
.
В заключение следует сказать, что в терминах линейных векторных пространств формулируются задачи математического программирования, и в частности, дискретного программирования, которое относят к задачам дискретной математики.