Покрытие и разбиение множеств

Разбиением множества А называется семейство А_i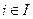непустых и различных подмножеств А, таких, что и для всех (i ≠ j). Множества A_i называютсяклассами разбиения.

Пример. Разбиения множества А = {1, 2, 3. 4}. {1, 2}, {3, 4} и {1}, {2, 4}, {3}. Все объединения разбиений дают множество А, а все их пересечения пусты.

Если множество А представляет собой объединение подмножеств А₁, А₂, ..., А_n ..., то совокупность подмножеств {А₁, А₂, ..., А_п, ...} называется покрытием множества А.

Пусть - некоторое семейство подмножеств множества M и 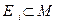. Семейство 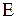называется покрытием множества M, если каждый элемент его принадлежит хотя бы одному из :

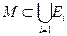
Семейство 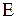называется дизъюнктным если элементы этого семейства попарно не пересекаются, т.е. каждый элемент множества M принадлежит не более чем одному из множеств :

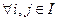
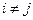
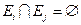
Дизъюнктное покрытие 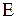называется разбиением множества M.

Если же совокупность подмножеств покрытия множества А такова, что при i ≠ j, то совокупность {А₁, А₂, ..., А_п, ...} называется разбиением множества А, а подмножества А_i — классами этого разбиения, (i = 1, 2, ... ,n, ...).

Пример

Пусть А — множество всех студентов МГСУ, которые его закончили, а А_i — подмножество тех студентов МГСУ, которые закончили i-й факультет этого вуза.

Поскольку не исключена возможность, что некто из множества студентов А закончил несколько факультетов данного вуза, и такой человек попадает в несколько соответствующих подмножеств совокупности, то ясно, что совокупность подмножеств А₁, А₂, …,A_k, является покрытием множества А.

Если же взять совокупностьвсех студентов МГСУ, которые учатся в данное время, то совокупность студентов А₁, А₂, …,A_k_` является, очевидно, разбиением множества всех студентов данного вуза, которые учатся в данное время.

Если все рассматриваемые множества являются подмножествами некоторого множества U, то это множество называютуниверсальным множеством.

Пример. Для арифметики универсальным множеством служит множество действительных чисел, так как натуральные, целые и рациональнее числа являются его подмножествами.

Рассмотрим два конечных множества А и В с числом элементов т и п. Между этими числами возможно одно из трех соотношений: т = п; т < п; т > п. Вопрос о том, какое из них имеет место, решается просто: подсчетом количества элементов А и В. Однако можно поступить иначе, не считая эти элементы. Для этого между элементами множеств А, В необходимо попытаться установить взаимно однозначное соответствие, при котором каждому элементу множества А отвечает один и только один элемент множества В и, наоборот, каждому элементу множества В соответствует один и только один элемент множества А.

Иными словами, каждому элементу множества А необходимо «поставить в пару» элемент множества В. Такое соответствие можно установить тогда и только тогда, когда число элементов в этих множествах одинаковое, т.е. т = п. Когда же после «постановки в пару» остались элементы множества В, то т < п. Если же полностью исчерпаны элементы В и остались лишние элементы множества А, то т > п.

Пример. Проверить, одинаково ли число студентов в группе и стульев в аудитории, можно не пересчитывая тех и других, посадить каждого студента на определенный стул. Если мест хватит всем и не останется ни одного лишнего стула, то тем самым будет установлено взаимно однозначное соответствие и, следовательно, равенство элементов в множествах студентов и стульев.

Если между элементами двух различных множеств А и В можно установить взаимно однозначное соответствие по любому закону, то эти множества называютсяэквивалентными, или равномощными. Это записывается так: А = В.

Характерно, что установление взаимно однозначного соответствия между элементами множеств пригодно для сравнениянетолько конечных множеств, но и бесконечных.

Приведем примеры эквивалентных бесконечных множеств. Множество всех натуральных чисел эквивалентно множеству всех четных чисел, так как каждому натуральному числу п соответствует одно и только одно четное число 2n, и каждому числу 2n соответствует его половина, являющаяся натуральным числом. Множество всех целых чисел эквивалентно множеству натуральных чисел. Соответствие между целыми и натуральными числами устанавливается по следующей схеме:

0,-1, 1.-2.2...

1, 2, 3, 4, 5,..., т.е. неотрицательному числу п > 0 ставится в соответствие нечетное число 2n + 1, а отрицательному п < 0- четное число 2 ׀n׀ .

Счетным множеством называется всякое множество, элементы которого можно поставить во взаимно однозначное соответствие со всеми числами натурального ряда. Иначе говоря, счетное множество — это такое множество, элементы которого можно последовательно пронумеровать числами натурального ряда. Приведенные выше примеры множеств четных и целых чисел являются счетными множествами,

Множество называется счетным, если оно эквивалентно множеству натуральных чисел.

Если эквивалентны между собой два конечных множества, то, как указывалось выше, они состоят из одинакового числа элементов.

Эквивалентные между собой бесконечные множества называются множествамиравной мощности.

Частично упорядоченные множества

Алгебраическое понятие решетки тесно связано с отношением порядка, заданным на конечном множестве, и может быть определено следующим образом.

Определение: Множество S называется частично упорядоченным (ЧУМ), если на нем задано рефлексивное, транзитивной и антисимметричное бинарное отношение частичного порядка с.

Определение: ЧУМ называется линейно упорядоченным (цепью), если для любых x,y ∈ S или x ≤ y, или y ≤ x, либо выполняются оба эти отношения (x = y).

Любое конечное, линейно упорядоченное множество (A, ≤) можно представить следующим образом: a₁ ≤ a₂ ≤ a₃ ≤. . .≤ a_n. Мы можем также записать A как (a₁, a₂, . . ., a_n). Линейно упорядоченное множество можно изобразить графически диаграммой, в которой элементам множества соответствуют вершины. Из вершины а ведет дуга в вершину b, если a ≤ b и нет такого с, что a ≤ c ≤ b. Конечному линейно упорядоченному множеству (A, ≤) соответствует диаграмма вида (рис. 3.1)

Рис. 3.1.

На таких диаграммах не принято изображать петли, отображающие рефлексивность отношения ≤, и дуги, отображающие транзитивность этого отношения.

Утверждение: Частичное упорядочение на конечном множестве может быть представлено как объединение отношений линейного порядка на некоторых подмножествах данного множества

Любой частичный порядок можно представить изображением объединения множества диаграмм соответствующих линейно упорядоченных подмножеств. Полученная таким образом диаграмма называется диаграммой Хасса.

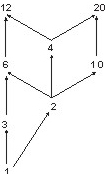
Рис. 3.2.

Пример 6.1.

Пусть на множестве S={1,2,3,4,6,10,12,20} задано отношение с={(x, y):х делитель y}. Выделим все линейно упорядоченные подмножества S: (1, 3, 6, 12), (1, 2, 6, 12), (1, 2, 4, 12), (1, 2, 4, 20), (1, 2, 10, 20). Объединение диаграмм, построенных для этих подмножеств, дает диаграмму Хассе, показанную на рис. 3.2. Если задано (S, ≤) и B – подмножество S: B ⊆ S, можно определить верхнюю и нижнюю грани подмножества В.

Определение: Верхней гранью двухэлементного подмножества B={a,b}, a,b ∈ S, называется элемент h ∈ S, такой, что a ≤ h, b ≤ h. Соответственно,

нижней гранью двухэлементного подмножества B={a, b}, a, b ∈ S, называется элемент l ∈ S, такой, что l ≤ a, l ≤ b.

Определение: Если некоторая из верхних граней H подмножества B={a,b} удовлетворяет неравенству H ≤ h, где h - произвольная верхняя грань подмножества B={a,b}, то ее называют наименьшей верхней гранью (supremum) подмножества B и обозначают H = sup ({a,b}). Соответственно, если некоторая из нижних граней L подмножества B = {a, b} удовлетворяет неравенству l ≤ L, где l - произвольная нижняя грань, то ее называют наибольшей нижней гранью (infimum) подмножества B и обозначают L = inf ({a,b}).

Введенные понятия хорошо иллюстрируются на языке диаграмм Хассе:

x ≤ y , если и только если на диаграмме существует путь из вершины x в вершину y; верхняя грань подмножества B={a,b} на диаграмме соответствует вершине, в которую есть путь как из a, так и из b; нижняя грань подмножества B={a,b} соответствует вершине, из которой есть путь как в a, так и в b.

Пример 6.2.

Рассмотрим ЧУМ, представленное диаграммой Хассе на рис. 6.2. Подмножество B={3,6} имеет две верхние грани: h₁=6 и h₂=12, одна из которых является наименьшей: H=sup({3,6})=h₁=6. Это же подмножество имеет две нижние грани:l₁=1 и l₂=3, одна из которых является наибольшей: L=inf({3,6})=l₂=3. Подмножество B={6,4} имеет одну верхнюю грань h₁=12, которая, естественно, будет наименьшей верхней гранью H=sup ({6,4})=12, и две нижние грани l₁=2, l₂=1, одна из которых будет наибольшей: L=inf ({6,4})=l₁= 2. Подмножество B={6,10} имеет те же две нижние грани l₁=2, l₂=1 и ту же наибольшую нижнюю грань L=inf ({6,10})=l₁= 2, однако не имеет ни одной верхней грани