Свойства бинарных отношений
Бинарное отношение R на множестве Хобладает следующими свойствами:
(а) рефлексивно, если хRхдля каждого 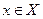 ,
,
Отношение R на множестве Х является рефлексивным, если оно выполняется между самим элементом, т.е. хRх. Пример, в отношениях «х имеет общий признак с у», «х похож на у» имеет место хRх, так как элемент х похож на самого себя.
- прямая x параллельна прямой y в плоскости z - хRх
- студент x ровесник студенту y – каждый студент сам себе ровесник хRх.
(а1) иррефлексивно, если хRхне имеетсмысла
- отношение строго порядка x <x на множестве действительных чисел – оно всегда ложно.
(а2) антирефлексивно, если хRхдля каждого 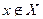 ,
,
Отношение R на множестве Х являетсяантирефлексивным, если хRх не выполняется ни для одного хX. Например, в отношениях «брат х старше брата у», «операция х выполняется раньше операции у», хRх не выполняется, так как брат хне может быть старше себя, а операция х начаться раньше самой себя.
(б) транзитивно, если  произвольных
произвольных 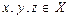 ,
,
Отношение R на множестве Х является транзитивным, если для всех  из соотношений хRу, уRz следует хRz. Например, в отношении «операция х предшествует операции y, а операция у предшествует операции z из хRу и уRz следует хRz.
из соотношений хRу, уRz следует хRz. Например, в отношении «операция х предшествует операции y, а операция у предшествует операции z из хRу и уRz следует хRz.
- город x связан с городом y шоссейной дорогой – между городом y и z
- студент x ровесник студенту y
- треугольник x подобен треугольнику y
- действительное число x больше действительного числа y
(в) симметрично, если 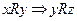 для произвольных
для произвольных 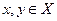 ,
,
Отношение R на множестве Х являетсясимметричным, если для всех х,у Х из хRу следует уRх. Например, в отношениях «хпохож на у», «операция хнесовместима с операцией у» имеет место как хRу, так и уRх. Действительно, если х похож на у, то у похож на х, если операция х несовместима с у, то операция у несовместима с х.
Х из хRу следует уRх. Например, в отношениях «хпохож на у», «операция хнесовместима с операцией у» имеет место как хRу, так и уRх. Действительно, если х похож на у, то у похож на х, если операция х несовместима с у, то операция у несовместима с х.
- прямая х перпендикулярна у (не рефлексивно).
- студент х приходится соседом у (не рефлексивно) .
(в1) антисимметрично, если  для произвольных
для произвольных 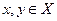 .
.
Отношение R на множестве Х являетсяантисиммитричным, если соотношения хRу и уRх выполняются тогда и только тогда, когда х = у для всех 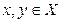 . Например, в отношении «операция х является частью операции у» имеет место хRу и уRх только тогда, когда х = у.
. Например, в отношении «операция х является частью операции у» имеет место хRу и уRх только тогда, когда х = у.
- бинарное отношение включения множеств
(в2) асимметрично, если  для произвольных
для произвольных 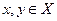 .
.
Отношение R на множестве Х является асимметричным, если из двух соотношений хRу, уRх одно не выполнено для всех 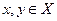 . Например, в отношениях «х подчиняется у», «операция х выполнена раньше операции у» имеет место хRу, но не выполняется уRх.
. Например, в отношениях «х подчиняется у», «операция х выполнена раньше операции у» имеет место хRу, но не выполняется уRх.
Помимо этих свойств на практике используются еще следующие:
- отношением эквивалентности,
- отношение толерантности
- отношения порядка.
Отношение эквивалентности
Отношение эквивалентности – это произвольное бинарное отношение R на множестве Х, обладающее свойствами:
- рефлексивности,
- транзитивности
- симметричности.
По смыслу отношение эквивалентности определяется как «элементы х и у одинаковы», «элементы х и у взаимозаменяемы».
В этом отношении каждый элемент эквивалентен самому себе (рефлексивность). Если элемент х эквивалентен элементу у, то и элемент у эквивалентен элементу х (симметричность). Если элемент х эквивалентен элементу у, а элемент у эквивалентен элементу z, то элемент х эквивалентен элементу z (транзитивность).
Лемма 1. Всякое разбиение множества А на классы задает на множестве А отношение эквивалентности.
Доказательство. Пусть 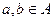 , положим aRb ↔a и b лежат в одном классе разбиения. Покажем, что полученное бинарное отношение является отношением эквивалентности. Для этого необходимо доказать, что оно рефлексивно, симметрично и транзитивно. Действительно. Поскольку a лежит в некотором классе разбиения, то aRa, т.е. оно рефлексивно.
, положим aRb ↔a и b лежат в одном классе разбиения. Покажем, что полученное бинарное отношение является отношением эквивалентности. Для этого необходимо доказать, что оно рефлексивно, симметрично и транзитивно. Действительно. Поскольку a лежит в некотором классе разбиения, то aRa, т.е. оно рефлексивно.
Пусть K – некоторый класс разбиения и  тогда и
тогда и  т.е aRb →bRa, Симметричность доказана.
т.е aRb →bRa, Симметричность доказана.
Из aRb →bRc следует  , Следовательно aRc, ч.т.д.
, Следовательно aRc, ч.т.д.
Лемма 2. Всякое отношение эквивалентности R, определенное на множестве А задает разбиение на классы.
Лемма 3. Между разбиениями множества на классы и отношениями эквивалентности, заданными на этом множестве , существует взаимно однозначное соответствие.
Пример 1. Отношение эквивалентности на множестве чисел является отношение равенства (=). Любое число а из множества действительных чисел равно самому себе a=a (рефлексивность). Если а=b, то b=а (симметричность). Если а=b, а b=с, то а=с (транзитивность).
Пример 2. Отношения параллельности прямых в эвклидовой плоскости.
Пример 3. Отношения проживания в одном доме жителей города.
Отношение эквивалентности разбивает любое множество на непересекающиеся подмножества (классы эквивалентности). В примере 3 все жители города разбиваются на жителей, живущих в одних и тех же домах. В результате получим столько классов эквивалентности, сколько домов, в которых проживают люди. Таким образом, если Мi, — i-й класс iI, а М — множество жителей, то  iIMi =M, Mi
iIMi =M, Mi Mj=
Mj= для всех i, j I ,где I — множество классов.
для всех i, j I ,где I — множество классов.
Примеры на эквивалентность
1. R - отношение равенства(=).
Отношение равенства x = y является эквивалентностью на любом множестве A, так как оно
рефлексивно (x = x),
симметрично (x = y  y = x),
y = x),
транзитивно (x = y & y = z  x = z).
x = z).
2. R - отношение подобия треугольников.
Отношение подобия на множестве треугольников является отношением эквивалентности.
рефлексивно (x = x),
симметрично (x = y  y = x),
y = x),
транзитивно (x = y & y = z  x = z).
x = z).
3. R - отношение равномощности.
На любом множестве B(U) отношение равномощности |A| = |B| является отношением эквивалентности. Для любых множеств A, B, C выполняются следующие свойства:
рефлексивно: (A ~ A поскольку idA : A ↔ A),
симметрично: если A ~ B, то B ~ A (так как из f: A ↔ B следует f-1: B ↔ A),
транзитивно: если A ~ B и B ~ C, то A ~ C (так как из f: A ↔ B, g: B ↔ C следует f◦g: A ↔ C).
4. R - отношение принадлежности.
Отношение принадлежности к одной студенческой группе на множестве студентов МГСУ является отношением эквивалентности.
рефлексивно (x = x),
симметрично (x = y  y = x),
y = x),
транзитивно (x = y & y = z  x = z).
x = z).
5. R - отношение вычисление одной и той же функции.
Пусть M – множество программ, вычисляющих одну и ту же функцию. Отношение E = {(x,y)| программы x и y вычисляют одну и ту же функцию} на множестве M является отношением эквивалентности.
рефлексивно (x = x),
симметрично (x = y  y = x),
y = x),
транзитивно (x = y & y = z  x = z).
x = z).
Отношениетолерантности
Отношение R на множестве Х называется отношениемтолерантности, если оно
- рефлексивно
- симметрично.
Пример. Отношение «игрок х играет сам с собой в шахматы и с другом у» есть отношение толерантности, так как хRх, а хRу влечет уRх.
Отношения порядка
А) Нестрогий порядок
Отношение R на множестве Х называется отношениемнестрого порядка, если оно
- рефлексивно,
- антисимметрично
- транзитивно.
Отношения ≤, ≥ на множестве чисел Х являются отношениями нестрогого порядка, так как любое число хХ равно самому себе (рефлексивность).
Для любой пары чисел х,уХ при а≤b не выполняется b≤a, а при а≥b не выполняется b≥a (антисимметричность).
Для любой тройки чисел х,у,zX, если а≤b и b≤с, то а≤с или, если а ≥b, b≥с, то а ≥с (транзитивность).
Б) Отношение частичной упорядоченности
Отношение частичной упорядоченности - это произвольное бинарное отношение, обладающее свойствами:
- рефлексивности,
- транзитивности
- антисимметричности.
Отношение частичной упорядоченности обычно обозначается через « ≤ », а пара <Х, ≤ > называется частично упорядоченным множеством. Будем применять также очевидные обозначения, такие как х ≥ у для у ≤ х, х <. у для 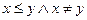 и т. д.
и т. д.
Примером частично упорядоченного множества может служить множество целых чисел с отношением делимости, множество целых (или вещественных) чисел с обычным отношением меньше или равно « ≤ », а также множество Р(X) с отношением включения  .
.
В) Отношениестрого порядка
Отношение R на множестве Х называется отношениемстрого порядка, если оно
- антирефлексивно,
- антисимметрично
- транзитивно.
Отношения <, > на множестве чисел Х являются отношениями строгого порядка, так как любое число хX не может быть меньше или больше самого себя (антирефлексивность).
Для любой пары чисел х, уX при х<у не может быть у<х, а при х>у не выполняется у>х (антисимметричность).
Для любой тройки чисел х,у,zX, если х<у, а у<z, то х< z, если х>у, а у> z, то х>z (транзитивность).
Множество Х с заданным на нем отношением нестрогого или строгого порядка R называетсяупорядоченным и обозначается парой <X, R>.
Если для каждой пары х, уX справедливо отношение строгого или нестрогого порядка, то множество <X, R> называетсяполностью упорядоченным. В противном случае множество <X, R> называется частично упорядоченным.
Строгий или нестрогий порядок, заданный на полностью упорядоченном множестве <X, R>, называетсялинейным порядком.
Пример 1. Все множества чисел линейно упорядочены, так как для любых чисел из этих множеств одно меньше другого или они равны.
Пример 2. Множество букв русского или латинского алфавита линейно упорядочено отношением предшествования, или, что то же, отношением следования.
Пример 3. Отношение подчиненности на некотором предприятии определяет строгий частичный порядок, так как в нем несравнимы сотрудники разных отделов.