Частично упорядоченные множества
Множество S называется частично упорядоченным (ЧУМ), если на нем задано рефлексивное, транзитивной и антисимметричное бинарное отношение частичного порядка с.
Частичным упорядочением (частичным порядком) в непустом множестве X называется всякое подмножество множества 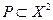 , удовлетворяющее следующим аксиомам:
, удовлетворяющее следующим аксиомам:
I. При любом 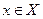 справедливо
справедливо 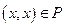 - рефлексивность отношений.
- рефлексивность отношений.
II. Если 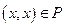 и
и 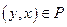 , то y = x - антисимметричность отношений.
, то y = x - антисимметричность отношений.
III. Если 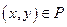 и
и 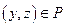 , то
, то 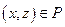 - транзитивность отношений.
- транзитивность отношений.
Часто вместо записи 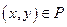 пишут x ≤ y или y ≥ x . Иногда вместо знака ≤ могут применять и другие похожие символы например
пишут x ≤ y или y ≥ x . Иногда вместо знака ≤ могут применять и другие похожие символы например 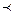 . Тогда аксиомы можно записать в виде:
. Тогда аксиомы можно записать в виде:
I. 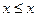 при всех справедливо
при всех справедливо 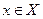 - рефлексивность отношений.
- рефлексивность отношений.
II. Если x ≤ y и y ≤ x, то y = x - антисимметричность отношений.
III. Если x ≤ y и y ≤ z, то x ≤ z - транзитивность отношений.
Эти соотношения называются неравенствами.
Частично упорядоченное множество – это некоторое множество X вместе с заданным на нем частичным порядком P, то есть пара (X, P).