Минимизации представления множества
Используя эти законы, рассмотрим задачу минимизации представления множества М с помощью операций 
, 
, не.
Под сложностью представления множества Мбудем понимать число символов Мi, неМi, в задающем его выражении.
Пусть в пространстве 1 = {М1, М2, М3} задано множество вида
М(М1, М2, М3) = неМ1неМ2неМ3неМ1неМ2М3неМ1М2неМ3М1неМ2неМ3М1М2неМ3М1М2М3 сложность которого равна 18.
На основании законов идемпотентности, коммутативности и ассоциативности объединения получаем
М(М1, М2, М3) = (неМ1неМ2неМ3неМ1неМ2М3) (неМ1неМ2неМ3М1неМ2неМ3) (неМ1неМ2неМ3М1неМ2неМ3) (М1неМ2неМ3М1М2неМ3) (М1неМ2неМ3М1М2М3)
Используя законы коммутативности пересечения и склеивания, имеем
.
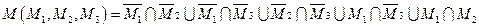Сложность представления уменьшилась до 10.
Согласно законам коммутативности объединения _и пересечения и закону склеивания получаем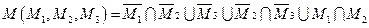 
Сложность представления уменьшилась до 7.
Согласно законам коммутативности пересечения и поглощения, имеем 
Сложность представления заданного множества уменьшилась от 18 до 5.
Последовательность применения законов будем называть стратегией преобразований. Сложность представления множества, получаемого в результате применения этих законов (каждый из которых определяет эквивалентное преобразование), зависит от используемой стратегии. Найдем стратегию, всегда порождающую минимальное выражение заданного множества.
Рассмотрим алгебру 
и определим множества, которые могут быть порождены (образованы) из произвольных подмножеств М1, М2,...,Мn, называемых порождающими или образующими пространства 1 с помощью операций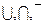 
.
Множество
i = 1,2, …n,
М, * = < , I = 1, 2,...,п,
в дальнейшем будем называть первичным термом.
Множество вида
sI = 0,1назовем конституентой.
Общее число различных конституент не превышает 2n. Каждой конституенте можно сопоставить двоичный набор длины п, число этих наборов равно 2n. Если некоторые конституенты равны 
, то общее количество конституент меньше 2n, при этом среди подмножеств найдутся хотя бы два такие, которые можно выразить одно через другое, т. е. зависимые. Например, если п = 2 и 
, то существуют только две отличные от конституенты
. 
, 
.
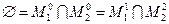Лемма 1.1. Пересечение двух различных конституент пусто.
Действительно, если конституенты 
и 
различны, то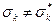 
по крайней мере для одного k, k £ n. Но тогда 
, следовательно. 
.
Лемма 1.2. Объединение всех конституент равно 1.
Представим 1 в виде
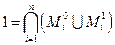
и, раскрыв скобки, в правой части равенства получим объединение всех конституент.
Контрольные вопросы
1. Что такое: декартово произведение множеств; декартова степень некоторого множества А; бинарное отношение, заданное на множестве А?
2. Что такое унарное отношение, приведите примеры.
3. Что такое бинарное отношение, приведите примеры.
4. Назовите основные свойства бинарных отношений.
5. Какое отношение называется рефлексивным, симметричным, антисимметричным, транзитивным?
6. Какое отношение называется отношением эквивалентности?
7. Дайте определение отображения множества А во множество В. Поясните термин «мощность множества».
8. Что такое сюръекция, инъекция, биекция?
9. Дайте определение функции.
10. Чему в математике служат отношения?
11. Как классифицируются отношения в зависимости от числа связей между элементами множества?
12. Дайте определение бинарного отношения.
13. Что представляет собой декартово произведение множеств?
14. Выпишите декартовы произведения множеств А = {а, b}, В = {1, 3}; декартового квадрата А = {1, а}.
15. Сколько элементов включает декартовый квадрат множества A = {1, 2,...,i, ...,n}?
16. Дайте определение бинарного, тернарного и n-арного отношения в терминах множеств.
17. Что понимают под рефлексивными и антирефлексивными отношениями?
18. Как характеризуются симметричные, асимметричные
и антисимметричные отношения?
19. Дайте определение транзитивного отношения.
20. Дайте определение отношения эквивалентности и приведите примеры.
21. Какое отношение называется отношением нестрогого порядка? Является ли отношение ≤ на множестве А = {1, 2, 3} отношением нестрогого порядка?
22. Какое отношение называется отношением строгого порядка?
23. Какое множество называется упорядоченным, полностью упорядоченным?
24. Что такое линейный порядок?
25. Дайте определение функции.
26. Является ли отношение R = {<1,а>, <1,b>, <2,а>}, определенное на декартовом произведении множеств А = {1,2}, B = {а, b}, функцией?
27. Является ли функция f(х) = х2 инъективной?
28. Что представляет собой функционал?
Лекция № 5
Из внимательного исследования частного случая может возникнуть общее понимание.
А. Пойа Математика и правдоподобные рассуждения. М.: Наука, 1975 с.