Размещения с повторениями

Пусть во множестве A имеются одинаковые (повторяющиеся) элементы. Размещениями с повторениями из n элементов по k называются кортежи длиной k, составленные из n-элементного множества A. Число этих кортежей обозначают 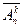. Черта указывает на возможность повторения элементов

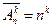
Пример.

Сколько пятизначных телефонных номеров можно составить из элементов множества {0,1,2,3,4,5,6,7,8,9}.

Решение.

Телефонные номера являются кортежами длиной k = 5, составленные из десятиэлементного множества с возвращением, т.е. для каждого из пяти элементов есть девять способов выбора.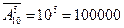

 

Рассмотрим размещения на языке множеств.

Даны множества X, Y, причем X = n, |Y| = m. Сколько существует функций: X —> Y, удовлетворяющих заданным ограничениям?

Элементы множества X соответствуют объектам, элементы множества Y — ящикам, а каждая функция f:. X —> Y определяет некоторое размещение, указывая для каждого объекта 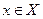ящик , в котором данный объект находится. Другую традиционную интерпретацию получим, трактуя Y как множество «цветов», а f(х) как «цвет объекта х». Наша задача, таким образом, эквивалентна вопросу, сколькими способами можно покрасить объекты так, чтобы были соблюдены некоторые ограничения.

Заметим, что без потери общности можем всегда считать, что Х = {1, ..., п} и Y = {1, ..., т}. Каждую функцию f можно тогда отождествить с последовательностью < f(1) , ,.., f (п)>.

Наша задача имеет самый простой вид, если не накладывается никаких ограничений на размещения. Имеет место следующая теорема.

Теорема 1.1. Если |X| = n, |Y| = m, то число всех функций f: X —> Y равно тⁿ.

Доказательство.

Считая, что Х = {1, ..., п}, сводим нашу задачу к вопросу о числе всех последовательности < y₁ ..., y_n > с членами из m-элементного множества Y. Каждый член последовательности y_i мы можем выбрать т способами, что дает тⁿ возможностей выбора последовательности < y₁ ..., y_n >.

Легко также найти число размещений, для которых каждый ящик содержит не более одного объекта — также размещения соответствуют взаимно однозначным функциям. Обозначим через |т|_п число всех взаимно однозначных функций из n-элементного множества в m-элементное множество.