Сочетания с повторениями

Полученные формулы справедливы только, когда в множестве A нет одинаковых элементов. Пусть имеются элементы n видов и из них составляется кортеж из k элементов среди которых могут быть одинаковые (повторяющиеся) элементы. Такие наборы называются сочетаниями с повторениями. Число таких сочетаний

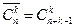
Пример.

Сколько наборов из 7 товаров можно составить, если имеется всего 4 вида.

Решение

Число наборов равно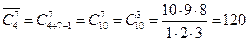

Комбинации элементов с повторениями

Пусть имеем неупорядоченное n-злементное множество A элементы которого разбиты на n классов (в каждом классе находится по одному элементу), которые будут называться типами элементов.

Комбинацией из n элементов по m с повторениями называется m-элементное подмножество множества A,каждый элемент которого принадлежит одному из n типов.Совокупность таких комбинаций называют комбинациями из n элементов по m

Теорема 1.2.8.Количество различных комбинаций из n элементов по m элементов с повторениями равно

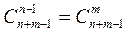
Доказательство.«Закодируем» каждую комбинацию следующим образом. Если комбинация включает k₁ элементов первого типа, то записываем подряд k₁ единиц, ставим нуль. После него ставим подряд k₂ единиц, если комбинация включает k₂ элементов другого типа и т.д.

Например, если A ={a, b, c, d}, то комбинациям по два элементас повторениями соответствуют пары {a,a}, {а,b}, {а,с}, {а,d}, {b,b}, {b, с}, {с,d}, {с,с}, {с,d}, {d,d}, аих "кодами" будут соответственно

11000, 10100, 10010, 10001,..., 00011.

Нетрудно убедиться, что между "кодами" и комбинациями существует взаимно однозначное соответствие (убедитесь самостоятельно).

Таким образом, каждой комбинации из п элементов по m соответствует последовательность из т единиц и п-1 нулей (в рассмотренном примере п = 4, т = 2). Следовательно, число всех комбинаций из п элементов по т с повторениями равно числу последовательно­стей, состоящих из т единиц и п - 1 нулей, т. е. 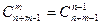. Теорема доказана.

Пример 1.2.7

Сколько целых неотрицательных решений имеет уравнение

x₁ + x₂ + ... + х_n = т? (1.2.4)

Решение. Решения данного уравнения можно интерпретировать так. Если имеем целые неотрицательные числа x₁, х₂, ..., x_п, такие что х₁ + х₂ + ... + x_п = т, то можно составить комбинацию из п элементов по т, взяв х_i элементов первого типа, х₂элементов второго типа, ..., x_п элемен­тов n-го типа.

Наоборот, имея комбинацию из п по т элементов, получим решение урав­нения (1.2.4) (x₁, х₂ ..., x_n - число элементов первого, второго, и, соответ­ственно, n-го типа), где все х_i неотрицательные (i = 1, 2, ..., n). Таким об­разом, между множеством всех неотрицательных решений уравнения (1.2.4) и множеством всех комбинаций из п элементов по т устанавлива­ется взаимно однозначное соответствие. Следовательно, число целых не­отрицательных решений уравнения (1.2.4) равно

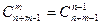
Например, если x₁ + x₂ + x₃ + х₄ = 10, то это уравнение имеет

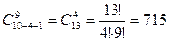
целых неотрицательных решений.