Алгебраическая система

Алгебраической системой A называется совокупность ‹M,O,R›, первая составляющая которой M есть непустое множество, вторая компонента O – множество алгебраической операций, третья компонента R – множество отношений на множестве M.

Пояснение.

1. Множество M алгебраической системы A называют несущим, или основным множеством.

2. Совокупность алгебраических операций и отношений алгебраической системы называют сигнатурой Σ. В этом случае алгебраическая система записывается парой ‹M, Σ.› .

3. Алгебраическая система ‹M,O› называется универсальной алгеброй (или просто алгеброй), если на основном множестве M множество отношений R пусто (т.е. R = ).

4. Алгебраическая система A = ‹M,R› называется реляционной системой (или моделью), если на основном множестве M заданы только отношения R (т.е. в этом случае пусто множество операций O, что означает O = ).

Пример 1. Алгебраической системой является аксиоматическая теория множеств ‹M, , -, › (где O = {, -} – множество из операций объединения и операций дополнения -, а R = {} – множество, состоящее из отношения включения .

Пример 2. Алгебра Кантора (алгебра множеств) - ‹B(M), , ›, несущим множеством является булеан B(A) (т.е. множество всех подмножеств данного множества U), а множеством операций O = {, , -} -, булевы операции объединения , пересечения и дополнения -.

Пример 3. Метрическое пространство ‹M,R›, где R – метрика, является реляционной системой. Пояснение. Пространство – множество объектов (точек) с введенным отношением между точками и операциями над элементами множества. Метрическое пространство – это множество точек Х с расстоянием между ними d≥0, удовлетворяющее трем аксиомам:

1. Аксиома идентичности. d=0 тогда и только тогда , когда x=y.

2. Аксиома симметрии. d(х,y)=d(y,x).

3. Аксиома треугольника. d(х,y)=d(y,z)+d(z,y),где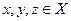

Расстояние d(х,y) называется метрикой, а пара ‹X,d› - метрическим пространством.