Множество и элементы множества
В настоящее время существующие теории множеств различаются парадигматикой (системой взглядов) концептуального базиса и логических средств. Так, в качестве примера, можем привести две противоположные точки зрения на первичное понятие "Множество".
Агрегатная точка зрения рассматривает множество как набор вещей (по Кантору), а с атрибутивной точки зрения множеством считается свойство (атрибут) вещи.
Символическая запись этих точек зрения следующая:
 (m есть элемент множества М).
(m есть элемент множества М).
m 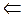 М (m обладает свойством М).
М (m обладает свойством М).
Здесь m, М – исходные неопределяемые (первичные) понятия "элемент" и "множество" а отношение принадлежности (инцидентности)  и предикации
и предикации 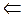 относятся к первичным (неопределяемым) отношениям.
относятся к первичным (неопределяемым) отношениям.
Фундаментальное понятие «множество», как первичное понятие, не имеет прямого определения, но, тем не менее, оно широко применяется в математике, например, точка, прямая и т.п.. При чем любое понятие дискретной математики можно определить с помощью понятия множества.
Согласно Г.Кантору (одному из основоположников "наивной" теории множеств), множеством (конечным или бесконечным), является неупорядоченная совокупность строго различимых (дискретных) объектов (агрегатов) для каждого из которых можно установить принадлежность его данному множеству.
Дискретная математика базируется на понятии множества. Мир является единым гармоничным целым, но для его анализа и исследования целесообразно его представлять как совокупность объектов. Выделение объектов производится мысленно или интуитивно по определенным признакам.
Пример. 1
А. По признаку принадлежности к МГСУ можно сформировать множество M – коллектив МГСУ.
Б. По признаку студент факультета ИСТАС создать множество S - студенты факультета ИСТАС.
В. Совокупности вершин и диагоналей в многоугольнике.
Г. Множество зайцев в лесу Московской области и т.д. и т.п.
Д. Решение квадратного уравнения есть множество, элементами которого являются корни заданного уравнения (алгоритмом установления принадлежности элемента множеству решений является его подстановка в квадратное уравнение).
Е. Все натуральные числа образуют бесконечное множество N: N = {1, 2, 3, 4, 5…….}
Ж. Все точки вещественной оси равномощно множеству всех действительных чисел 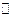 .
.
З. Множество, не содержащее элементов, есть пустое множество  = {}.
= {}.
Таким образом, объекты, объединенные по определенному признаку, образуют множество.
Как правило, множество обозначается большой буквой, часто, латинского алфавита (M, S и т.п.), а элементы, составляющие этого множества одноименными прописными буквами (m, s и т.п.).
Определение множества
Объекты, обладающие схожими свойствами (характеристиками) можно объединить в группы.
Множество - это любое объединение или совокупность объектов, объединенных по определенным признакам (характеристикам).
Или можно сказать, что множество - это совокупность вполне определенных и различимых между собой объектов любой природы, мыслимых как единое целое. Это определение полезно сопоставить с определением системы поскольку в дальнейшем придется много заниматься с системы.
Пример. 2. Общепринятые стандартные обозначения наиболее важных множеств:
N - Множество целых положительных (натуральных) чисел - (1, 2, 3, 4, . . . ).
Z - Множество всех целых чисел - (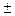 1,
1, 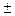 2,
2, 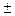 3,
3, 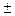 4, . . . ).
4, . . . ).
Q - Множество рациональных чисел.
R - Множество вещественных чисел.
C - Множество комплексных чисел.
P - Множество простых чисел (2, 5, 7, 11,. . . , . . . ).
E2 - Множество, состоящее из нуля и единицы (0, 1).
Pn - Множество булевых функций n аргументов.
На протяжении изучения всего курса будем стараться придерживаться этих обозначений.
Замечание:
Элементами множества могут быть множества.
Термин "множество" есть экспликация интуитивно явных понятий "класс", "семейство", "ансамбль", ets.
Термин "элемент" множества есть экспликация интуитивно явных понятий "участие", "член", "представитель".
Не следует связывать понятие множество с обыденным представлением о множестве, как о большом количестве. Так множество {х} есть синглетон, а пустое множество не содержит элементов.
Элементы множества не обязательно должны существовать одновременно. Так, следующие три объекта пространства-времени:
- студент, вчера сдавший зачет,
- он же, сегодня защитивший курсовой проект,
- он же, намеревающийся завтра сдать экзамен
образуют множество из трех элементов.
Предостережение:
Можно говорить о множестве снежинок (дождинок) при снегопаде (дожде), но нельзя говорить о множестве снежинок (дождинок) в сугробе (луже), (так как в последнем случае нет дискретности).