Замыкание и подалгебры

Подмножество 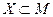называется замкнутым относительно операции φ, если

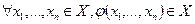
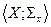Если X замкнуто относительно всех , то называется подалгеброй алгебры , где , k = n_i/

Пример 1. Алгебра - поле действительных чисел.

Тип – (2,2).

Все конечные подмножества, кроме {0}, не замкнуты относительно сложения и все конечные подмножества, кроме {0} и {0,1}, не замкнуты относительно умножение.

Кольцо целых чисел образует подалгебру рациональных и, соответственно, вещественных чисел.

Пример 2. Алгебра - алгебра подмножеств над множеством M.

Тип – (2,2,1).

При этом 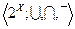- подалгебра.

Пример 3. Алгебра гладких функций , где 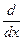- операция дифференцирования.

Множество полиномов одной переменной x образует подалгебру которая обозначается R[x].

Тип – (1).

 

Теорема. Непустое пересечение подалгебр образует подалгебру.

Доказательство. Пусть - подалгебра алгебры . Тогда

 

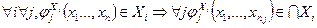
Замыканием множества 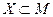относительно сигнатуры Σ (обозначается [X]_Σ) называется множество всех элементов (включая сами элементы X), которые можно получить из X, применяя операции из Σ.