Доказательство

1. Каждая дуга входит в какой-то узел. Из п. 2 определения 9.2.1 имеем:

v V {r } d⁺(r) = 1, где r — корень. Следовательно, q = р - 1.

2. Пусть G — ордерево, граф G' получен из G забыванием ориентации рёбер, r — корень. Тогда v₁, v₂V (v₁, r)G' &(r, v₂)G', следовательно, v₁, v₂ (v₁, v₂) и граф G' связен. Таким образом, учитывая п. 4. теоремы 9.1.2, G'-дерево.

3. Следует из пункта 2.

4. От противного. Если бы в G существовали два пути из и в v, то в G' имелся бы цикл.

5. Пусть G_v — правильный подграф, определяемый множеством узлов, достижимых из v. Тогда d_Gv⁺(v) = 0, иначе узел v был бы достижим из какого-то узла v'G_v, и, таким образом, в G_v, а значит, и в G имелся бы контур, что противоречит пункту 3. Далее имеем: v' G_v {v} d⁺(v') = 1, так как G_v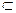G. Все узлы G_v достижимы из v по построению. По определению 9.2.1 получаем, что G_v — ордерево.

6. Пусть вершина r назначена корнем и дуги последовательно ориентированы «от корня» обходом в глубину. Тогда d⁺(r) = 0 по построению;

vV - d⁺(v) = 1, так как входящая дуга появляется при первом посещении узла; все узлы достижимы из корня, так как обход в глубину посещает все вершины связного графа. Таким образом, по определению 9.2.1 получаем ордерево.

 

Следствие. Алгоритм поиска в глубину строит ордерево с корнем в начальном узле.

Каждое свободное дерево определяет не более р ориентированных деревьев. Таким образом, общее число различных ордеревьев с р узлами не более чем в р раз превосходит общее число различных свободных деревьев с р вершинами

Концевая вершина ордерева называется листом. Путь из корня в лист называется ветвью. Длина наибольшей ветви ордерева называется высотой. Уровень узла ордерева — это расстояние от корня до узла. Сам корень имеет уровень 0. Узлы одного уровня образуют ярус дерева.

Замечание

Наряду с «растительной» применяется еще и «генеалогическая» терминология. Узлы, достижимые из узла и, называются потомками узла и (потомки образуют поддерево). Если в дереве существует дуга (u, v), то узел и называется отцом (или родителем) узла v, а узел v называется сыном узла и. Сыновья одного узла называются братьями.

 

Эквивалентное определение ордерева

Ордерево Т — это конечное множество узлов, таких что:

1. Имеется один узел r, называемый корнем данного дерева.

2. Остальные узлы (исключая корень) содержатся в k; попарно непересекающихся множествах Т₁,... , Т_k каждое из которых является ордеревом (k ≥ 0).