А1A2A3| + … + |А1A2A3| + … + |А1A2An| + … + |Аn-2An-1An| + (-1)n-1 |А1A2A3…An|.
Конечное множество А имеет мощность k, если оно равномощно отрезку 1.. k;:
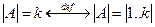 .
.
Если множество А конечно, |А| = k, то элементы А всегда можно перенумеровать, то есть поставить в соответствие элементам номера из отрезка 1..k с помощью некоторой процедуры. Наличие такой процедуры подразумевается, когда употребляется запись А = {а1,...,аk}.
По определению 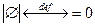 .
.
Мощность множества М это число его элементов, обозначается как 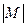 . Здесь |М| - количество элементов конечного множества М, в дальнейшем называемое мощностью множества
. Здесь |М| - количество элементов конечного множества М, в дальнейшем называемое мощностью множества
Пример.
Множество натуральных чисел бесконечно, 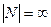 |, поскольку оно равномощно своему собственному подмножеству чётных чисел.
|, поскольку оно равномощно своему собственному подмножеству чётных чисел.
ТЕОРЕМА 1 Любое непустое конечное множество равномощно некоторому отрезку натурального ряда:
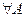
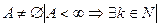 |А| = |1...k|.
|А| = |1...k|.
доказательство
Рассмотрим следующую программу.
i = 0 { счётчик элементов }
wihle  do
do
select 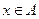 { выбираем элемент }
{ выбираем элемент }
i = i + 1 { увеличиваем счётчик }
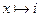 { ставим элементу в соответствие номер }
{ ставим элементу в соответствие номер }
А: = А - x { и удаляем элемент из множества }
end while
Если эта процедура не заканчивает работу, то она даёт соответствие А ~ N. что невозможно ввиду конечности А. Значит, процедура заканчивает работу при i = k. Но в этом случае построено взаимно-однозначное соответствие А~1..k.
ТЕОРЕМА 2 Любой отрезок натурального ряда конечен:
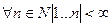 .
.
доказательство
От противного. Пусть существуют бесконечные отрезки натурального ряда. Рассмотрим наименьшее п такое, что |1..п| = ∞. Тогда отрезок 1..п, равномощен некоторому своему собственному подмножеству А, |1..п| = |А|, то есть существует взаимно-однозначное соответствие f из отрезка 1..п в подмножество А. I: Обозначим 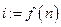 . Рассмотрим соответствие из отрезка 1..n-1 в его собственное множество А - i, задаваемое следующим правилом:
. Рассмотрим соответствие из отрезка 1..n-1 в его собственное множество А - i, задаваемое следующим правилом:
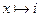 if f(x) < i then f(x) else f(x) -1 end if.
if f(x) < i then f(x) else f(x) -1 end if.
Это соответствие является взаимно однозначным, а значит, отрезок 1..n-1 является бесконечным, что противоречит выбору п.
СЛЕДСТВИЕ Различные отрезки натурального ряда неравномощны:
п≠т=> 1..п ≠ |1..т|.
доказательство
Пусть для определённости п > т. Тогда 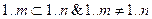 . Если |1..п| = |1..т|, то |1..т| = ∞, что противоречит теореме.
. Если |1..п| = |1..т|, то |1..т| = ∞, что противоречит теореме.
Пример.
Условия равенства (неравенства) множеств
Множества Ма и Мb совпадают (равны),если у них одни и те же элементы. Символически это запишется следующим образом
Ма = Мb  Ма
Ма 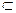 Мb и Мb
Мb и Мb 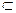 Ма
Ма
Если множество Мa - подмножество множества Мb и множество Мb - подмножество множества Мa, то оба этих множества состоят из одних и тех же элементов. Такие множества называются равными: Ма = Мb,.