F5 – повторение по y
f6 – сумма по модулю 2 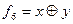
f7 – дизъюнкция 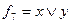
f8 – стрелка Пирса 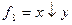
f9 – эквивалентность 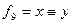
f10 – отрицание y
f11 – импликация от y к x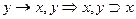
f12 – отрицание x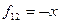
f13 – импликация от x к y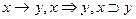
f14 – штрих Шеффера 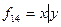
f15 - константа 1.
Для инженера ВТ алгебра логики (ВТ – алгебра переключательных схем или комбинационная логика) является системой алгебраических методов решения логических задач, а также совокупных задач, решаемых такими методами; для ВТ - это инструмент синтеза комбинационных схем, являющихся частным случаем конечных ????, элементной базой которого является либо функциональные элементы,
Предметом двузначной алгебры логики явл. однородные двузначные логические и операции над ними, а также вытекающие из их свойств правила преобразования
(упрощение, минимизация) с целью алгоритмизации решения задач.
В алгебре логики высказывания рассматриваются только с точки зрения истинности или ложности без рассматривания их смысла.
Индекс функции fi(x, y) является десятичным эквивалентом двоичного числа, образованного из вектора значений функции на упорядоченном множестве наборов значений аргументов: {(0,0),(0,1),(1,0),(1,1)}. Функции f0, f3, f5, f10, f12, f15 являются расширением на случай двух переменных уже известных функций одной переменной. Функции f1(x,y) = x ∨ y (конъюнкция) и f7(x,y) = x ∧ y (дизъюнкция) совместно с функцией инверсии (f10, f12) были использованы в предыдущих разделах для построения форм представления переключательных функций, пригодных для аналитической записи переключательных функций произвольной сложности.
Рассмотрим более подробно эти функции. Две из них f0 = 0 и f15 = 1 являются константами. Наиболее важные функции двух переменных имеют специальные названия и обозначения. Заметим, что эти обозначения не всегда общеприняты.
Перечислим 7 важнейших функций:
1) конъюнкция (функция И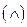 ) двух высказываний X и Y называется высказывание X
) двух высказываний X и Y называется высказывание X Y, которое истинно только в том случае, когда X и Y оба истинны.
Y, которое истинно только в том случае, когда X и Y оба истинны.
Таблица истинности для конъюнкций
| X | Y | X Y Y
|
Заметим, что конъюнкция – это фактически обычное умножение (нулей и единиц). Иногда эту функцию обозначают X&Y или X Y.
Y.
2) дизъюнкция (функция ИЛИ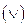 ) двух высказываний X и Y называется высказывание X
) двух высказываний X и Y называется высказывание X Y, которое истинно только в том случае, когда X и Y оба истинны.
Y, которое истинно только в том случае, когда X и Y оба истинны.
Таблица истинности для дизъюнкций
| X | Y | X Y Y
|
3) импликация (следование) двух высказываний X и Y называется высказывание X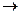 Y, которое истинно тогда и только тогда, когда X истинно, а Y ложно.
Y, которое истинно тогда и только тогда, когда X истинно, а Y ложно.
Таблица истинности для импликации
| X | Y | X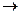 Y Y
|
Иногда импликацию обозначают x→y (читается “из x следует y”).
Это очень важная функция, особенно в логике. Ее можно рассматривать следующим образом: если х = 0 (т.е. х “ложно”), то из этого факта можно вывести и “ложь”, и “истину” (и это будет правильно), если у = 1 (т. е. у “истинно”), то истина выводится и из “лжи” и из “истины”, и это тоже правильно. Только вывод “из истины ложь” является неверным. Заметим, что любая теорема всегда фактически содержит эту логическую функцию.
4) сложение по модулю 2 (здесь и далее, если не оговорено противное, знаком 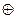 будем обозначать такое сложение) двух высказываний X и Y называется высказывание X
будем обозначать такое сложение) двух высказываний X и Y называется высказывание X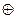 Y, которое истинно тогда и только тогда, когда X истинно, а Y ложно или X ложно, а Y истинно. Сумма по модулю два, или антиэквивалентность, по определению
Y, которое истинно тогда и только тогда, когда X истинно, а Y ложно или X ложно, а Y истинно. Сумма по модулю два, или антиэквивалентность, по определению 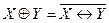
Таблица истинности для импликации
| X | Y | X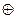 Y Y
|
5) эквивалентность или подобие двух высказываний X и Y называется высказывание X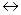 Y, которое истинно тогда и только тогда, когда X и Y оба истинны или ложны.
Y, которое истинно тогда и только тогда, когда X и Y оба истинны или ложны.
Таблица истинности для эквивалентности
| X | Y | X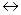 Y Y
|
Эта f9 = 1 тогда и только тогда, когда х = у. Заметим, что будем применять оба обозначения: ху (в основном при изучении функций) и х ~ у (когда речь будет идти о логических операциях).
6) штрих Шеффера двух высказываний X и Y называется высказывание 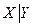 , которое ложно только, когда оба высказывания истины. По определению штрих Шеффера является антиконъюнкцией
, которое ложно только, когда оба высказывания истины. По определению штрих Шеффера является антиконъюнкцией 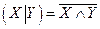 .
.
Таблица истинности для штриха Шеффера (антиконъюнкции)
| X | Y | 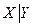
|
Иногда эту функцию называют “не и” (так как она равна отрицанию конъюнкции).
Замечание. Конъюнкция, дизъюнкция, отрицание были определены для объектов, принимающих лишь два значения 0 и 1. Однако бывают случаи, когда можно ввести такие операции для некоторых других объектов (эти операции также называют иногда конъюнкцией, дизъюнкцией и отрицанием), для которых также выполнены свойства 1–6. В этом случае говорят, что на этих объектах введена булева алгебра.
7) стрелка Пирса (иногда эту функцию называют штрих Лукасевича) двух высказываний X и Y называется высказывание 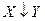 , которое истинно только, когда оба высказывания ложны. По определению стрелка Пирса (штрих Лукасевича) является антидизъюнкцией
, которое истинно только, когда оба высказывания ложны. По определению стрелка Пирса (штрих Лукасевича) является антидизъюнкцией 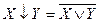 .
.
Таблица истинности для стрелки Пирса (антидизъюнкцией)
| X | Y | 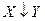
|
Эта функция является отрицанием дизъюнкции и поэтому иногда ее называют “не или”.
Заметим, что свойства последних двух функций (как будет видно далее) похожи между собой и, может быть, поэтому в литературе их часто путают (т. е. называют f8 штрихом Шеффера, а f14 – стрелкой Пирса).
Замечание. Во всех вышеприведенных таблицах истинности логических операций число строк 2n, где n – число простых высказываний.
Три оставшиеся функции, (f2 , f4 и f11) особого значения в дискретной математике не имеют.
Заметим, что часто будут рассматриваться функции от функций, т. е. суперпозиции перечисленных выше функций. При этом последовательность действий указывается (как обычно) скобками. Исключение составляет конъюнкция (которая на самом деле является обычным умножением в двоичной системе). Поэтому конъюнкция совершается первой, даже если отсутствуют скобки. Например, запись xy yz означает (xy)
yz означает (xy)  (yz).
(yz).
Из перечисленных функций особую роль играют три функции, а именно конъюнкция, дизъюнкция и отрицание, поэтому рассмотрим более подробно их свойства.
Помимо этих связок используются еще три связки полученные из вышеуказанных связок
| Название | Прочтение | Обозначение |
| Штрих Шеффера | Антиконъюнкция | 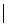
|
| Стрелка Пирса | Антидизъюнкция | 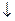
|
| Сумма по модулю два | Антиэквивалентность | 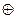
|
Штрих Шеффера 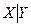 или антиконъюнкция, по определению
или антиконъюнкция, по определению 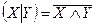
Стрелка Пирса 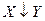 или антидизъюнкция, по определению
или антидизъюнкция, по определению 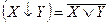
Сумма по модулю два 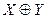 или антиэквивалентность, по определению
или антиэквивалентность, по определению 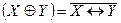
Таблицы истинности этих операций
| X | Y | Штрих Шеффера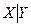
| Стрелка Пирса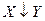
| Сумма по модулю 2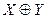
|