Эквивалентность формул
Различные формулы могут иметь одинаковые таблицы истинности. Так возникает понятие эквивалентности формул.
Формулы φ(x1,..., xn) и ψ(x1,..., xn) называются эквивалентными (φ ~ ψ), если совпадают их таблицы истинности, т. е. совпадают представляемые этими формулами функции fφ(x1,..., xn) и fψ(x1,..., xn)
Пример 1. Проверка на эквивалентность следующих формул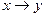 
и 
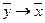. Построим таблицы истинности формул 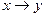и ,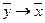
| x | y |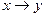
|
|
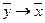
убеждаемся в том, что 
~ 
. Действительно это отношение ~ является отношением эквивалентности, т. е. оно рефлексивно (φ ~ φ), симметрично (φ ~ ψ) => (ψ ~ φ) и транзитивно (φ ~ ψ, ψ ~ χ => φ ~ χ).
Основные эквивалентности между формулами:
1. 
~ 
; 
~ 
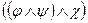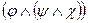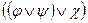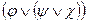- (ассоциативность 
и 
).
2. 
~ 
; 
~ 
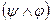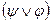- (коммутативность и ).
3. 
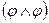~ φ;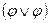 
~ φ - (идемпотентность и ).
4. 
~ 
; 
~ 
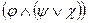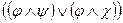- (законы дистрибутивности и ).
5. 
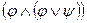~ φ;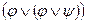 
~ φ - (законы поглощения и ).
6. 
~ 
; 
~ 
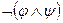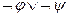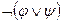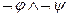- (законы де Моргана).
7. 
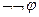~ φ; - (закон двойного отрицания - инволютивность).
8. 
~ 
;
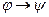9. 
~ 
;
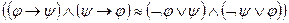10. 
~ 
; 
~ 
;
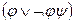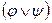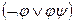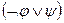11. 
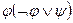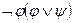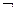~ φψ; 
~ 
φψ.
11. Закон склеивания: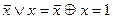 
.
12. Для функций: конъюнкция, дизъюнкция и сумма по модулю два справедливы следующие тождества:
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
;
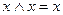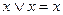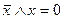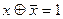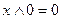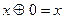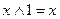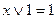13. Для функций конъюнкция и дизъюнкция справедливы тождества:
;
;
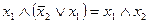Для доказательства справедливости любых из приведенных тождеств нужно составить таблицы истинности для булевых функций.
Булеву функцию любого числа переменных можно задать формулой, содержащей функции одной и двух переменных посредством подстановки одних булевых функций вместо переменных в другие булевы функции, т. е. посредством суперпозиции булевых функций.
Формула φ(x1,..., xn) называется выполнимой (опровержимой), если существует такой набор значений переменных, при котором формула принимает значение 1 (соответственно 0).
Пример 1. Формула ху является одновременно выполнимой и опровержимой, поскольку 00 = 0, а 11 = 1.
Формула φ(x1,..., xn) называется тождественно истинной, общезначимой или тавтологией, если эта формула принимает значение 1 при всех наборах значений переменных, т. е. функция f является константой 1.
Пример 2. Формула 
является тождественно истинной, одновременно выполнимой 01 = 1, 11 = 1.
Формула φ(x1,..., xn) называется тождественно ложной или противоречием, если эта формула принимает значение 0 при всех наборах значений переменных, т. е. функция f является константой 0.
Пример 3. Формула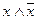 
является тождественно опровержимой, поскольку 00 = 0, а 01 = 0.
Если φ - тождественно истинная формула, то будем писать |= φ Пример.|= . В противном случае пишем |
φ. Пример |.
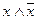Очевидным является следующее