Алгоритм приведения формулы к ДНФ.

1. Выразить все логические операции, участвующие в построении формулы, через дизъюнкции, конъюнкции и отрицания, используя эквивалентности

~

~

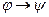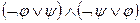
и определения операций:

штрих Шеффера (антиконъюнкция) ,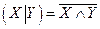

стрелки Пирса (антидизъюнкция)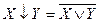

сумма по модулю два (антиэквивалентность) .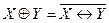

2. Используя законы де Моргана, переносим все отрицания к переменным и сокращаем двойные отрицания по правилу

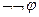~ φ

3. Используя закон дистрибутивности

~ ,

преобразуем формулу так, чтобы все конъюнкции выполнялись раньше дизъюнкций. В результате применения пп. 1-3 получается ДНФ данной формулы.

 

Пример 6. Привести к ДНФ формулу .

Решение. Выразим логические операци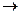и и 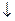через , и :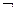

φ ~ ~ ~ .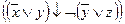

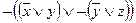В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:

φ ~ ~ ~ .

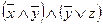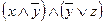Используя закон дистрибутивности, приводим формулу к ДНФ:

φ ~ .

 

Приведение формулы к КНФ производится аналогично приведению ее к ДНФ, только вместо п. 3 применяется пункт

3'. Используя закон дистрибутивности ~ , преобразуем формулу так, чтобы все дизъюнкции выполнялись раньше, чем конъюнкции.

 

Пример 6. Привести к КНФ формулу ,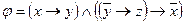

Решение. Преобразуем формулу φ к формуле, не содержащей :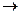

φ ~ ~

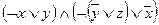
В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания: φ ~ ~

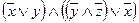
По закону дистрибутивности получаем, что формула φ эквивалентна формуле

φ ~ ,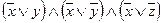

являющейся КНФ.

Упростим полученную формулу:

1) используем закон дистрибутивности

~

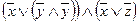
2) используем закон эквивалентность φφ₀ ~ φ,

~

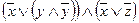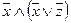
3) используем закон поглощения

~ .

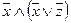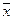Таким образом, формула φ из примера 6.1.1 эквивалентными преобразованиями приводится к формуле 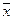(являющейся одновременно ДНФ и КНФ формулы φ).

~ ~ ~

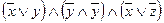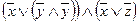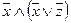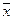
Построить таблицу истинности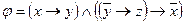

 

Любая булева функция может иметь бесконечно много представлений в виде ДНФ и КНФ. Особое место среди этих представлений занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ).