Системы булевых функций
Пусть даны булевы функции f(g1, g2, …, gm) и g1(x1, x2, …, xn), g2(x1, x2, …, xn), … , gm(x1, x2, …, xn). Подставим функции gi в функцию f . Получим новую булеву функцию
f(и g1(x1, x2, …, xn,), g2(x1, x2, …, xn,), …, gm(x1, x2, …, xn,)),
которую называют суперпозицией функций f и gi (i = 1,2,…m), т.е. при помощи операции суперпозиции получили новую булеву функцию.
Набор булевых функций M = { f1, f2, … ,fk} называется полной системой булевых функций или базисом, если любая булева функция выражается через них при помощи операции суперпозиции в конечном числе раз.
Пример.
Набор булевых функций:
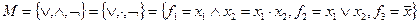
является полной системой булевых функций, так как любая булева функция может быть аналитически представлена в форме СДНФ или СКНФ.
Эту полную систему называют стандартным базисом.
Пример.
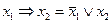
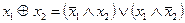
Теорема (о двух системах)
Пусть имеется полная система булевых функций M = { f1, f2, … ,fm}. Тогда для полноты некоторой другой системы булевых функций N = { g1, g2, … ,gn} необходимо и достаточно, чтобы любая функция 
выражалась через функции системы N при помощи операции суперпозиции.
Доказательство.
Необходимость очевидна. (Почему?)
Достаточность. Рассмотрим произвольную булеву функцию h. Тогда она выражается через функции при помощи операции суперпозиции в силу полноты системы M. Но, в свою очередь, любая функция выражается через функции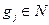 
при помощи операции суперпозиции. Следовательно, можно через функции gj выразить любую булеву функцию, и, значит, система N полна.