ЛОГИКА ВЫСКАЗЫВАНИЙ
Математическая логика изучает базовые понятия синтаксиса (формы) и семантики (содержания) естественного языка. Рассмотрим три крупных направления исследований в математической логике — логику высказываний, логику предикатов и теорию доказательств. Эти направления потребуются при изучении кибернетических и интеллектуальных систем.
Известно, что в исчислении высказываний теоремами являются общезначимые формулы, поэтому автоматизация доказательства осуществляется в виде проверки общезначимости формул с помощью таблиц истинности. Проверка истинности формул производится для любого конечного набора значений переменных. Таким образом, можно алгоритмизировать процесс доказательства теорем, но не процесс вывода теорем из аксиом.
Определения
Определение 1. Высказыванием называется повествовательное предложение (текст) естественного языка, о котором имеет смысл говорить истинно оно или ложно.
Например, «студент Петров присутствует на лекции», «эта стена белая», «33 = 28» и т.д.
Предложение «Город х стоит на реке у» не является высказыванием, пока не заданы х и у, так как здесь нельзя определить истина это или ложь.
Из данных высказываний можно составлять новые, сложные высказывания с помощью так называемых логических операций.
Истинность значений сложных высказываний определяется только истинностью значений составляющих высказываний, а не их смыслом. Простейшие высказывания, в которых не выделяются части, являющиеся высказываниями, будем обозначать прописными латинскими буквами А, В, ..., Р, ... и называть атомарными.
Определение 2. Отрицанием высказывания Р называется высказывание, истинное тогда и только тогда, когда Р ложно. Отрицание Р обозначается ]Р или Р и читается «не Р».
Отрицание высказывания определяется табл. 1.
Таблица истинности отрицания
| P | 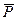
|
| И | Л |
| Л | И |
В естественном языке отрицание соответствует составлению из высказывания Р нового высказывания «неверно, что Р», или «не Р».
Определение 3. Конъюнкцией двух высказываний Р и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания. Конъюнкция Р и Q обозначается Р & Q или Р  Q и читается «Р и Q».
Q и читается «Р и Q».
Конъюнкция определяется
Таблица истинности конъюнкции
| P | Q | 
|
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
В естественном языке конъюнкция соответствует соединению высказываний союзом «и».
Определение 4. Дизъюнкцией двух высказываний Р и Q называется высказывание ложное тогда и только тогда, когда ложны оба эти высказывания.
Дизъюнкция высказываний Р и Q обозначается Р V Q и читается «Р или Q».
Дизъюнкция определяется табл. 3.
Таблица 3.
Таблица истинности конъюнкции
| P | Q | 
|
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
В естественном языке дизъюнкция соответствует соединению высказываний союзом «или» в неразделительном смысле.
Рассмотрим теперь сложное высказывание, которое в естественном языке выражают, например, фразой «если Р, то Q» (или «из Р следует Q», или «Р влечет Q»). Жизненный опыт подсказывает, что истинность этого высказывания должна обозначать следующее:
если Р истинно, Q «обязано» быть истинным (следовать из Р);
если же Р ложно, то на Q нет ограничений, оно может быть как истинным, так и ложным (из ложного утверждения ничего не следует).
Значит, «из Р следует Q» ложно в единственном случае: Р истинно, Q ложно.
Следующие высказывания служат примерами:
1) если 0 = 0, то 1 = 1;
2) если 0 = 1, то 0 = 0;
3) если 0 = 0, то 0 = 1;
4) если 0 = 1, то 1 = 2.
Первое утверждение истинно, так как, используя равенство 0 = 0 и другие свойства чисел, можно вывести 1 = 1, прибавляя по единице к обеим частям равенства 0 = 0.
Второе утверждение тоже естественно считать истинным, так как, умножая на нуль обе части равенства 0 = 1, получим 0 = 0.
Третье приходится считать ложным, так как исходя из истинного равенства 0 = 0 с помощью умозаключений никогда не придем к ложному.
Четвертое естественно считать истинным. Прибавляя к обеим частям равенства 0 = 1 по 1, получим 1 = 2.
Используя оборот «если Р, то Q» как логическую операцию, определим ее следующим образом.
Определение 5. Импликацией двух высказываний Р и Q называется высказывание ложное тогда и только тогда, когда Р истинно, a Q ложно.
Импликация высказываний обозначается Р => Q, или Р  Q и читается: «Р влечет Q», или «если Р то Q», или «из Р следует Q», или «пусть Р, тогда Q», или «Р является достаточным для Q», или «Q является необходимым для Р».
Q и читается: «Р влечет Q», или «если Р то Q», или «из Р следует Q», или «пусть Р, тогда Q», или «Р является достаточным для Q», или «Q является необходимым для Р».
Высказывание Р называется посылкой импликации, a Q -заключением.
Таблица 4. Таблица истинности импликации и эквивалентности
| P | Q | 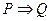
| 
|
| И | И | И | И |
| И | Л | Л | Л |
| Л | И | И | Л |
| Л | Л | И | И |
Определение 6. Эквивалентностью двух высказываний Р и Q называется высказывание, истинное тогда и только тогда, когда истинности Р и Q совпадают. Эквивалентность обозначается Р ~ Q и читается: «Р эквивалентно Q», или «Р тогда и только тогда, когда Q», или «Р является необходимым и достаточным для Q».
Формулы логики высказываний
Теперь перейдем к понятию формулы логики высказываний. Среди способов задания множеств рассматривался процедурный, или рекурсивный. Формулы логики высказываний образуют перечислимое множество, которое зададим рекурсивным способом.
Определение 7. Алфавитом называется любое непустое множество. Элементы этого множества называются символами (буквами) данного алфавита.
Определение 8. Словом в данном алфавите называется произвольная конечная последовательность символов (возможно, пустая).
Слово а называется подсловом слова b, если b = b1 a b2 для некоторых слов b1 и b2.
Всякое подмножество слов данного алфавита называется языком в этом алфавите.
Рассмотрим язык логики высказываний, т. е. подмножество слов в некотором выделенном алфавите. Слова в языке логики высказываний принято называть формулами логики высказываний. Эти формулы используются для моделирования высказываний.
Определение 9. Пусть известно.
1. Алфавит логики высказываний содержит следующие символы: высказывателъные переменные Х1, Х2, логические связки &,  ,
, 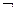 , =>, ~; символы скобок (, ), которые в дальнейшем будут играть разные роли.
, =>, ~; символы скобок (, ), которые в дальнейшем будут играть разные роли.
2. Всякая высказывательная переменная есть формула, которая называется атомарной.
3. Если а — формула, то (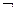 а) — формула. Если а и b — формулы, то (а&b), (а V b), (а => b), (а ~ b) — формулы.
а) — формула. Если а и b — формулы, то (а&b), (а V b), (а => b), (а ~ b) — формулы.
4. Других правил образования формул нет.
Замечание 1. Вместо высказывательных переменных Х1, . . ., Хп, ... иногда удобно пользоваться прописными латинскими буквами без индексов.
Пример 1. Слово (((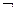 А)&В) => (B
А)&В) => (B А)) — формула.
А)) — формула.
Слово (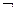 А & В) => В
А & В) => В  A не является формулой (нет скобок).
A не является формулой (нет скобок).
Слово ((А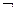 В) => (В
В) => (В  A)) — не формула, так как знак
A)) — не формула, так как знак 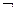 не бинарная связка.
не бинарная связка.
Замечание 2. Удобно при записи формул по умолчанию опускать внешние скобки и скобки при отрицании высказывательных переменных, например формула из примера 1:
(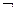 А&В) => (В
А&В) => (В  A).
A).
Определение 10. Логические связки в логике высказываний задают алгебраические операции на множестве Ф всех высказываний.
Отрицание — унарная алгебраическая операция, остальные четыре логические связки: конъюнкция, дизъюнкция, импликация, эквивалентность - бинарные алгебраические операции.
В связи с этим логика высказываний — алгебра с пятью алгебраическими операциями (Ф, &, V, =>, ~, 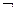 ), которая называется алгеброй логики высказываний.
), которая называется алгеброй логики высказываний.
Обсудим синтаксис, семантику и прагматику языка логики высказываний.
Синтаксис языка логики высказываний изучает правильность написания формул (слов языка), согласно определению формулы логики высказываний. Нетрудно предложить алгоритм отыскания ошибок в слове, например, указать на символ не из алфавита логики высказываний, на отсутствие необходимого или присутствие лишнего операнда логической операции, на отсутствие или несоответствие скобок в слове и т. д.
Семантика языка логики высказываний изучает смысл формул (слов языка) с точки зрения их оценивания на истинность. Вопросы семантики часто решаются с помощью таблиц истинности формул.
Прагматика языка логики высказываний изучает цели (задачи) использования тех или иных формул языка. Вопросы прагматики решаются в рамках функционирования (назначения) кибернетических и интеллектуальных систем, в которых используется логика высказываний.
Правила преобразования формул
Определение 11. Пусть а и b — две формулы, зависящие от одного и того же множества высказывательных переменных.
Эти формулы называются равносильными, если на любой оценке переменных они принимают одинаковые значения.
Равносильность формул а и b логики высказываний будем обозначать a ≡ b, так же как равносильность формул в элементарной алгебре, например a3 — b3 ≡ (a - b)(a2 + ab + b ).
Пояснение. Оценка переменных — набор истинностных значений данных переменных.
Равносильность формул имеет свой алгебраический аналог в тождественном равенстве алгебраических выражений.
Замечание. Нужно различать символы «≡» и «~».
Символ «~» является символом логической операции формального языка (это необходимо и достаточно).
Символ «≡» является метасимволом. Он не принадлежит алфавиту языка логики высказываний и говорит о равносильности слов с точки зрения их семантики.
Основные равносильности.
Для любых формул a, b, c справедливы следующие равносильности.
1. a&b=b&a (коммутативность операции &).
2. a&a = а (идемпотентность операции &).
3. а & (b & с) = (а & b) & с (ассоциативность операции &).
4. а  b = b
b = b  а (коммутативность операции
а (коммутативность операции  ).
).
5. а  а = а (идемпотентность операции
а = а (идемпотентность операции  ).
).
6. а  (b
(b  с) = (а
с) = (а  b)
b)  с (ассоциативность операции
с (ассоциативность операции  ).
).
7. a (b&с) = (а
(b&с) = (а b)&(a
b)&(a с) (дистрибутивность операции
с) (дистрибутивность операции  относительно операции &).
относительно операции &).
8. a&(b с) = (a&b)
с) = (a&b) (а&с) (дистрибутивность операции & относительно операции
(а&с) (дистрибутивность операции & относительно операции  ).
).
9. а & (а  b) = а (первый закон поглощения).
b) = а (первый закон поглощения).
10. а  (а&b) = а (второй закон поглощения).
(а&b) = а (второй закон поглощения).
11. 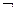
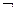 а = а (снятие двойного отрицания).
а = а (снятие двойного отрицания).
12.  (a&b) =
(a&b) = 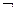 a
a
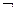 b (первый закон де Моргана).
b (первый закон де Моргана).
13.  (а
(а  b) =
b) =  а &
а & b (второй закон де Моргана).
b (второй закон де Моргана).
14. а = (a&b) (а&
(а&  b) (первая формула расщепления).
b) (первая формула расщепления).
15. а = (a b)&(а
b)&(а
 b) (вторая формула расщепления).
b) (вторая формула расщепления).
Любая из этих равносильностей легко может быть доказана с помощью таблиц истинности.
Еще одна группа равносильностей показывает, что одни связки могут быть выражены через другие.
16. а ~ b ≡ (а  b)&(b
b)&(b а) ≡ (a&b)
а) ≡ (a&b)  (
(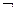 a&
a&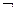 b).
b).
17. a=>b≡ a
a b≡
b≡ (a&
(a& b).
b).
18. a b≡
b≡ a
a b≡
b≡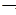 (
( a&
a& b).
b).
19. a&b≡ (a =>
(a => b) ≡
b) ≡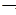 (
( a&
a& b).
b).
Рассмотрим доказательство приведенных равносильностей на примерах тождеств 8, 10, 15. При этом в методических целях приведем три различных способа доказательства.
Пусть в тождестве 8 формулы a, b, с — атомарные, т. е. a = А, b = B, с = С.
Таблица 6
Таблица истинности равносильных формул
| A | B | C | 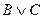
| 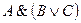
| 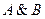
| 
| 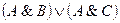
|
| И | И | И | И | И | И | И | И |
| И | И | Л | И | И | Л | И | И |
| И | Л | И | И | И | Л | И | И |
| И | Л | Л | Л | Л | Л | Л | Л |
| Л | И | И | И | Л | Л | Л | Л |
| Л | И | Л | И | Л | Л | Л | Л |
| Л | Л | И | И | Л | Л | Л | Л |
| Л | Л | Л | Л | Л | Л | Л | Л |
Рассмотрим табл. 6. Пятый и восьмой столбцы в таблице совпадают, следовательно, тождество доказано. Этот способ доказательства равносильности назовем табличным.
Теперь докажем тождество 10 (второй закон поглощения) путем логических рассуждений. Этот способ называется логическим. Он имеет два хода рассуждения: «слева—направо» и «справа — налево».
Ход «слева —направо». Пусть в тождестве 10 слева будет ложь, т.е. а  (а&b) = Л. Тогда по определению дизъюнкции будет: а = Л и (а&b) = Л. Тем самым получили, что справа в тождестве 10 имеем ложь: а = Л.
(а&b) = Л. Тогда по определению дизъюнкции будет: а = Л и (а&b) = Л. Тем самым получили, что справа в тождестве 10 имеем ложь: а = Л.
Ход «справа— налево». Пусть в тождестве 10 справа будет ложь, т. е. a = Л. Тогда для левой части тождества 10 имеем ложь. В самом деле (а&b) = Л. Тем самым а  (а&b) = Л.
(а&b) = Л.
Тождество 10 полностью доказано. Рассматривать отдельно случай, когда слева и справа в данном тождестве истина нет необходимости, так как его доказательство можно провести рассуждением от противного и использованием уже доказанного.
Например, пусть слева в тождестве — истина, тогда и справа будет истина, так как в противном случае, если справа будет ложь, то, по доказанному, слева будет ложь. А это противоречит предположению. Аналогично рассматривается случай «справа- налево».
Итак, в логическом способе доказательства равносильности достаточно рассматривать один случай — или для истины, или для лжи, но обязательно в два хода: «слева — направо» и «справа— налево».
Теперь докажем тождество 15 (вторая формула расщепления) третьим способом, который назовем алгебраическим.
Суть способа состоит в использовании уже доказанных равносильностей для преобразования левой и правой частей тождества к одному и тому же виду.
Рассмотрим правую часть тождества 15. Воспользуемся тождеством 7, которое предполагаем доказанным. Тогда вынесем а за скобки, будем иметь (a b)&(а
b)&(а
 b)≡а
b)≡а (b&
(b& b) ≡ а, так как (b&
b) ≡ а, так как (b& b) ≡Л.
b) ≡Л.
Тем самым правая часть тождества 15 преобразована в левую и равносильность доказана.
Рассмотрим правила, с помощью которых удобно переходить от одних равносильностей к другим.
Теорема 1 (правило равносильных добавлений и удалений формул).
Если а, b и с — произвольные формулы, то следующие равносильности выполняются и не выполняются одновременно:
a ≡ b;  a ≡
a ≡  b;
b;
a&с ≡ b&с; с&a ≡с&b;
a с≡b
с≡b с; с
с; с a≡ c
a≡ c b;
b;
a => с≡ b => с; с => a ≡ с =b;