Следование и эквиваленция

Высказывательная форма Q₂ следу­ет из высказывательной формы Q₁, если импликация Q₁→Q₂ об­ращается в истинное высказывание при любых наборах значений переменных, входящих в нее. Для операции логического следова­ния принято обозначение .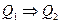

Пусть даны предикаты Q₁(x₁, х₂, …, х_n) и Q₂(x₁, х₂, …, х_n), а их множества истинности соответственно T(Q₁) и T(Q₂). Поскольку 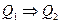, то если 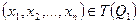, т.е. Q₁ истинна, то должна быть истинна Q₂, т.е. 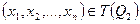. Поскольку такое свойство должно быть у любого элемента из T(Q₁), то это опреде­ление подмножества. Итак, .

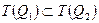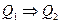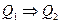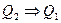Пусть даны два предиката, определенные на одном множестве. Высказывательные формы Q₁ и Q₂ назовем равносильными, если при любом наборе значений переменных, входящих в них, вы­сказывательные формы принимают одинаковые значения истин­ности: . Очевидно, что если , a то 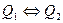. Тогда T(Q₁) = T(Q₂). т.е. множества истинности равносильных предикатов также совпадают.

Пример.

Пусть высказывательные формы заданы на множестве действительных чисел R.

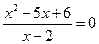и х² - 5х + 6 = 0 не являются равносильными.

 

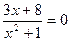и Зх + 8 = 0 являются равносильными.

 

ln (х - 1) + ln (х + 1) = 2 и ln (х² - 1) = 2 не являются равносиль­ными.

 

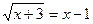их+3 = (х-1)² не являются равносильными.

 

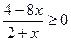и (4 - 8х)(2 + х) > 0 не являются равносильными.

 

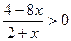и (4 - 8х)(2 + х) > 0 являются равносильными.

 

и не являются равносильными.

В математике нарушение цепочки тождественных преобразова­ний при решении уравнений или неравенств влечет за собой по­терю имеющихся или приобретение посторонних корней, т.е. из­менение множества истинности исследуемого предиката.

 

Можно доказать, что отношение равносильности высказывательных форм обладает известными свойствами, а именно, оно рефлективно и симметрично. В том случае, когда одинаковые перемен­ные в каждой из исследуемых форм принимают значения из од­ного множества, отношение равносильности будет обладать также и свойством транзитивности.

Тогда назовем равносильным преобразованием высказывательной формы Q₁ ее замену на равносильную форму Q₂. Две равносиль­ные высказывательные формы с одинаковым набором перемен­ных, для которых установлен одинаковый порядок, определяют один и тот же предикат.

Эти свойства предиката используются при решении уравне­ний и неравенств, которые тоже являются некоторыми высказывательными формами. Так, решение любого уравнения или неравенства предусматривает установление множества его истин­ности, т.е. множества истинности соответствующего ему преди­ката. В процессе поиска множества истинности производят замену одного предиката другим, равносильным данному, с целью упро­щения имеющихся высказывательных форм.

Пример.

2х - 13 + х² - (6х² - 4х + 5 - 6х²) = 0 <=> 6х = 18 <=> х = 3, т. е. множество истинности каждого из этих уравнений состоит из одного числа 3.

Рассмотрим примеры, для которых областью определения яв­ляется множество действительных чисел: D = Е.

Пример.

Для двух высказывательных форм — уравнений (х - 2)(х - 3) = 0 (Q₁) и х - 3 = 0 (Q₂) — из х - 3 = 0 следует, что (х - 2)(х - 3) = 0, т.е. верна запись 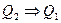. Однако из (х- 2)(х- 3) = 0 не следует х - 3 = 0. Например, х = 2 является корнем первого уравнения, но не второго.

Пример.

Из уравнения (х - 5)(х - 2) = 0 следует неравенство х > 0, так как корни уравнения — числа 2 и 5 — удовлетворяют также и неравенству.

Пример.

Тождественно-истинное высказывание х² + 5 > 0 может следо­вать из любой высказывательной формы Q, имеющей непустое множество истинности 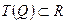, т.е. форма Q→ (х² + 5 > 0) истинна при любых значениях х.

 

Отношения следования и равносильности для высказывательных форм, вообще говоря, зависят от того множества, на котором оно рассматривается.

Пример.

Высказывательная форма х > 9 следует из неравенства 8 < х < 12, если D = {2, 0, 4, 5, 7, 9, 10, 11, 13}, но не следует, если D(Q) = N. Действительно, при D = {2, 0, 4, 5, 7, 9, 10, 11}T(Q₁) = {9, 10, 11}, a T(Q₂) = {9, 10, 11, 13} и выполняется 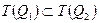, т.е. форма Q₁ → Q₂ истинна.

Во вто­ром случае (D(Q) = N), T(Q₁) = {8, 9, 10, 11}, a T(Q₂) = {9, 10, 11, 12, 13, 14 ...}, но отношение T(Q₁) с T(Q₂) не выполняется, поскольку .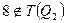

 

Правила вывода исчисления предикатов:

Правило заключения (modus ponens) — правило, аналогичное тому, которое введено в исчислении высказываний.

Правило обобщения (-введения, ug-правило) R₂: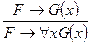, где G(x) содержит свободные вхождения х, тогда как F не содержит свободных x.

 

Правило -введения (eg-правило) R₃: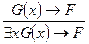

 

Нарушение этих требований может привести к ложным выво­дам, полученным из истинных высказываний.

 

Пример.

Даны предикаты Р(х): «натуральное х делится на 15», Q(x): «х делится на 5». Высказывание Р(х)→Q(x) истинно для любых хN. Приме­ним для него правило обобщения. Имеем Р(х) →x Q(x): «Если х делится на 15, то каждое число х делится на 5». Получили ложное утверждение, так как правило -введения применимо к 0-мест­ным, а не к одноместным, как Р(х), предикатам.

 

Можно доказанные теоремы делать новыми правилами вывода. Так, помимо правил - и -введения можно ввести правила уда­ления кванторов.

Пусть выведена или дана формула xF(x), например «Суще­ствуют студенты, работающие по специальности». Из предметно­го множества всех студентов выберем такого, о котором действи­тельно известно, что он работает по специальности, и для него введем константу а. Поэтому xF(x) → F(a). Это так называемое правило -удаления, или es-правило (правило выбора).

Правило -удаления снимает квантор общности, осуществляя переход от xF(x) к произвольным формулам F(a), F(y) и др. с учетом того, что эти переменные свободны от х в Fx.

Пример.

Из высказывания «Каждый студент колледжа владеет компьюте­ром» будет следовать, что конкретный студент Максимов тоже владеет компьютером, и произвольно выбранный некоторый сту­дент у владеет компьютером, и всякий студент z тоже владеет компьютером. При этом необходимо помнить, что предметные переменные у и z не должны быть связанными.

 

Правило -удале­ния называют правилом универсальной конкретизации, или us-npaвилом.

 

Примеры.

1. «Все металлы (М) — плавятся (П). Цинк (Ц) — металл. Зна­чит, цинк плавится». Формализация в логике предикатов примет вид: x(M(x) →П(х)) x(Ц(x)→ М(х))├ x(Ц(x)→ М(х)). Снятие квантора общности: (М(х) → П(х)) (Ц(х) → П(х)); тогда на основании транзитивности импликации имеем (Ц(х) →М(х)), (М(х) → П(х)) ├ Ц(х) → П(х).

Вывод x(Ц(x) →П(х)) — обобщение по R₂ — верен.

 

2. «Все студенты (С) проходят практику (П). Некоторые студен­ты работают в фирме (Ф), значит, некоторые работающие в фир­ме — проходят практику». Формализация примет вид: x(C(x) → П(х)) х(С(х) Ф(х)) ├ х(Ф(х) П(х)). Уберем кванторы по правилам us и es. Имеем (С (a) → П(а))(С(a)Ф(а)) (С (а) → П(а))С (а)Ф(a) П(а)Ф(а).

Вывод: х(П(х)Ф(х)), т.е. существуют студенты, которые проходят практику в фирме.

 

Свойства отношения классификации

Рассмотрим непустое мно­жество U. Пусть дана одноместная высказывательная форма Ф с переменной, которая принимает значения из U, проявляя свой­ство некоторых объектов из него и соответствуя некоторому пре­дикату Q. Множество истинности T(Q) таких объектов является подмножеством Uкак универсального множества.

Пример.

Пусть дано U_x = {5, 6, 7, 8, 9, 10, 11, 12, 13, 14 ...}.

Высказывательной форме «5 < х < 12» соответствует подмножество

T₁(Q) = {5, 6, 7, 8, 9, 10, 11} (T(Q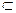₁)U₁).

Из множества U₂ = {1, 3, 5, 7, 9, 11, 13, 15} та же высказывательная форма выделяет множество истинности Т₂( Q) = {5, 7, 9, 11},

из U₃ = {5, 6, 7, 8, 9, 10, 11} - T₃ (Q) = U₃,

из U₄ = = {12, 13, 14, 15} рассматриваемая высказывательная форма выде­ляет пустое подмножество истинности T₄(Q) = .

Эта высказывательная форма выражает на множестве U един­ственное свойство, характерное для рассматриваемого предиката на заданном множестве U, т. е. одноместный предикат Q (в дан­ном случае «5 < х < 12») задает свойство данного множества. Тогда множество элементов, обладающих таким свойством Q, будем называть объемом этого свойства.

 

Если на множестве U задан предикат, выражающий некоторое свойство Р, то множество U можно разбить на два подмножества Т(Р) и UT(P). Такое разбиение на непере­секающиеся подмножества мы называем классификацией множе­ства U по основанию Р.

Пример.

Так, в предыдущем примере Т(Р) = {5, 6, 7, 8, 9, 10, 11} множество истинности предиката Р: «5 < х < 12» из множества U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}. UT(P) = {1, 2, 3, 4, 12, 13, 14, 15}.

 

Пусть на множестве U задано еще одно свойство Q. Тогда все множество U, разбиваясь на четыре подмножества, представляет новую классификацию. С помощью логических операций такую классификацию записывают в виде: .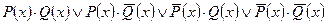

Замечание. Это аналогично разложению булевой функции по двум переменным (см. подразд. 4.7), с той разницей, что каждое слагаемое должно иметь вид 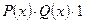, так как мы разлагаем формулу исчисления предикатов, имеющую вид тавтологии.

 

Пример.

Так, в предыдущем примере Т(Р) = {5, 6, 7, 8, 9, 10, 11} множество истинности предиката Р: «5 < х < 12» из множества U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}. UT(P) = {1, 2, 3, 4, 12, 13, 14, 15}.

Пусть в нашем примере предикат Q выражает новое свойство — «быть нечетным числом». Тогда эти два свойства одновременно классифицируют множество U на подмножества:

Т(Р)T(Q) = {5, 7, 9, 11}, выполнено Р(х)∙Q(x);

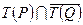= {6, 8, 10}, выполнено ;

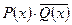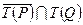= {1, 3, 13, 15}, выполнено ,

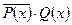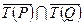= {2, 4, 12, 14}, выполнено .

 

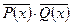Уточним понятие «отношение» с помощью понятия «преди­кат». Во всех n-местных предикатах (n > 2) устанавливаются неко­торые отношения между переменными.

 

Примеры.

1. Высказывательная форма «х — друг у» выделяет из всего мно­жества людей пары х и у, которые связаны между собой отноше­нием дружбы.

2. Высказывательная форма «х ┴ у» выделяет из множества пар прямых, например на плоскости, те пары, которые связаны от­ношением перпендикулярности.

3. Высказывательная форма «х² + у² + z² = 16» выделяет из всего множества троек координат те, которые связаны отношением «точ­ка с координатами (х; у; z) лежит на сфере с центром в начале координат и радиусом R = 4».

 

Отрицания в исчислении предикатов

В разговорной речи для построения отрицания обычно перед сказуемым ставят частицу не.

Пример,

1а «Студент х учится на факультете программирова­ния» имеет отрицание

16 «Студент х не учится на факультете про­граммирования».

 

? Но всегда ли построенное таким образом отрицание истинно?

Утверждения 2а «Все выпускники колледжей продолжили об­разование в вузе» и 2б «Все выпускники колледжей не продолжи­ли образование в вузе» не являются отрицанием друг друга, так как они оба ложны.

Пары утверждений За «Некоторые выпускники колледжей про­должили образование в вузе» и 36 «Некоторые выпускники кол­леджей не продолжили образование в вузе» тоже не служат отри­цанием друг друга, так как они оба истинны.

Вторая и третья пары утверждений отличаются от первых тем, что содержат кванторные слова «все» и «некоторые». А при пост­роении отрицаний для предложений, содержащих кванторы, прием введения отрицания не перед сказуемым не срабатывает.

Можно воспользоваться другим, универсальным, приемом построения отрицаний предложений, содержащих кванторы, добавив общее отрицание неверно, что... Тогда во втором примере «Неверно, что все выпускники колледжей продолжили образование в вузе» со­впадает по смыслу с утверждением «Некоторые выпускники кол­леджей не продолжили образование в вузе». Таким образом, отри­цанием предложения 2а служит 36, а отрицанием За служит 26.

 

Символически общее отрицание принято записывать с помо­щью либо общей черты, либо отрицания самого квантора.

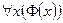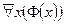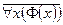Для отрицания предложения_возможны записи , или , или : ;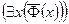

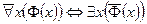для отрица­ния 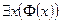аналогично: 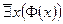, или ,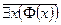

или : .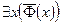

 

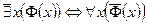Эти равносильности являются обоснованием метода по­строения отрицаний высказываний, содержащих кванторы. Для построения отрицания высказываний, содержащих квантор 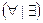, достаточно заменить его на другой квантор 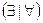и взять отрицание выражения, на которое этот квантор был «навешен».

Для многоместных кванторов также применяется это правило: осуществляется последовательный перенос отрицания с кванторного слова на предложение, стоящее за квантором, а сам квантор заменяют на двойственный.

Например, для формулы 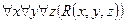построим отрицание: 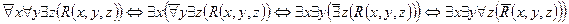. В подразд. 4.8 была показана булева двойственность конъюнкции и дизъюнкции. Поэтому для сложных высказываний, состоящих из простых, раз­деленных операциями конъюнкции и дизъюнкции, отрицание стро­ится следующим образом: нужно все кванторы 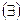заменить на 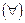, и наоборот; все связки и () заменить на или (), и наоборот; и взять отрицание утверждения.

Контрольные вопросы

1. Что называется предикатом? Приведите примеры предикатов.

2. Какой предикат называется разрешимым, тождественно истинным. Тождественно ложным?

3. Перечислите операции, которые можно осуществить над предикатами. Как применяются предикаты в алгебре? Что такое множество истинности предиката?

4. Из чего состоит алфавит логики предикатов? Что такое квантор?

5. Что называется формулой логики предикатов?

6. Сформулируйте основные правила построения формул.

7. В чем состоит смысл термина «интерпретация» в логике предикатов?

8. Сформулируйте основные правила перехода к новым равносильным формулам.

9. Какая формула называется непротиворечивой, противоречивой, общезначимой?

10. Какая формула называется приведенной? Что такое приведенная форма?

11. Какая формула называется нормальной формой? Сформулируйте алгоритм приведения формулы к нормальной форме.

12. Что называют исчислением предикатов?

13. Сформулируйте аксиомы исчисления предикатов.