Р е ш е н и е н е л и н е й н ы х у р а в н е н и й м е т о д о м х о р д

 

Метод хорд является более быстрым способом нахождения корня уравнения f (x)=0 , нежели метод половинного деления (Рис. 1).

Пусть функция f(x) непрерывна на отрезке ( а , в ) и f ( а ) f ( в ) < 0.

Для определения корня в первом приближении проведем прямую через две точки ( а , f (а) ) и ( в , f (в) ) и найдем точку пересечения x этой прямой с осью абсцисс . Если ½f(x)½ £ e , где e - малое число , опреде-ляющее точность решения уравнения, то х принимается за корень уравнения

 

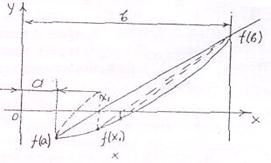
Рис. 1

Если ½f(x)½ > e , то находится произведение f(a)f (x). Если f (а) f (x)>0 , то за неподвижный конец хорд принимается точка ( в, f(в)), если f(а) f(x) < 0 , то - точка ( а , f( а )). Снова проведем хорду, которая пересечет ось

абсцисс ближе к точке пересечения кривой f(x) с осью x. При f (а) f(x) > 0 хорда проводится через точки ( x, f(x) , (в, f( в ) ) , т . е . роль точки а играет точка ( x, f(x)) . Чтобы получить координаты точки пересечения новой хорды с осью xдостаточно в первоначальном уравнении хорды « а » заменить на x, а f(а) - на f(x) . Аналогично обстоит дело и в случае f(а) f(x) <0.

Теперь получим аналитическое выражение изложенных выше словесных рассуждений . Уравнение прямой , проходящей через заданные две точки , имеет вид

=

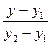
Разрешим это уравнение относительно x:

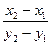
x -x=(y -y)

Учитывая, что в точке пересечения хорды с осью x у=0 , получаем:

x= x- y(x- x) / (y- y)

 

По условию у =f(а); у= f(в), x= а; x= в.

С учетом этого получаем:

 

x= а - f(а ) ( в - а ) / ( f(в ) - f( а) ) ( 1 )

По этой формуле вычисляется значение корня уравнения в первом приближении. Проверяем точность вычисленного корня. Если £ e, то вычисления прекращаются. Если f(x)> e , то вычисляется произведение f(а) f(x) . Если f(а) f(x) > 0 , то принимается а = x f(а) = f(x) и по этим данным по формуле ( 1 ) вычисляется новое значение х. Если же f(a)f(x)<0 , то принимается в =x, f(в)=f(x) и по этим данным вычисляется новое значение х. Так продолжается до тех пор, пока не будет выполняться неравенство f (x) £ e, или пока два последовательных значения x не будут отличаться не более, чем на e, т.е. 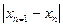£ e₁ . На основе этого алгоритма составлена подпрограмма H O R D , текст которой приведен в приложении 3 .

Пример решения уравнения методом хорд приведен также в приложении 3 .