Контрольная работа Введение в математический анализ

Контрольная работа «Введение в математический анализ»

З а д а ч а 1

Если то Если то . Если то - неопределенность.

Пример 1

Вычислить предел .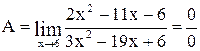

.

Найдем корни многочленов

.

 

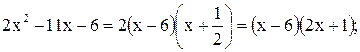
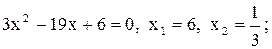
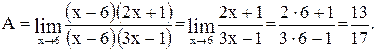
Контрольные варианты к задаче 1

Вычислить пределы функции:

 

.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.
.	.	.

 

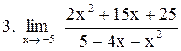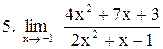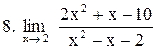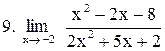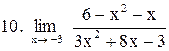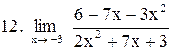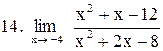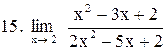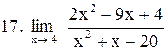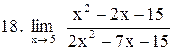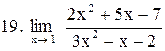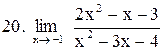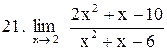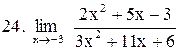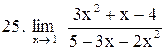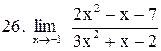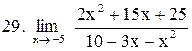З а д а ч а 2

Пример 2

Вычислить предел .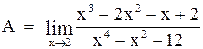

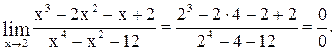
В числителе и знаменателе получаются нули за счет сомножителя 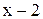, который стремится к нулю при 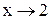. Разложим многочлены на множители, разделив их на

.

-

-

.

 

-

-

-

-

.

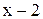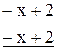
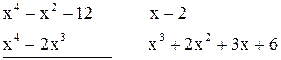
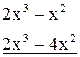
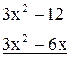
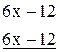
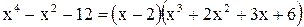Замечание.При разложении многочлена в числителе можно было применить способ группировки и вынесения общего множителя, а в знаменателе найти корни, решив биквадратное уравнение.

 

Контрольные варианты к задаче 2

Вычислить пределы функций:

 

.	.
.	.
.	.
.	.
. .	.
.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
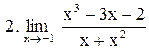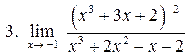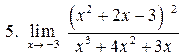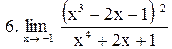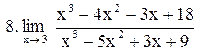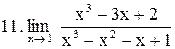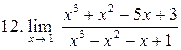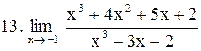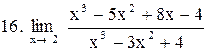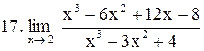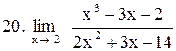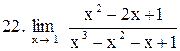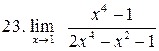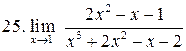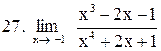.	28. .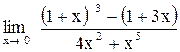
.	.

 

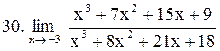З а д а ч а 3

Если в числителе или знаменателе стоят иррациональные выражения, то для получения сомножителя умножим числитель и знаменатель на сопряженные им выражения.

 

Пример 3

Вычислить .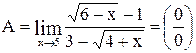

 

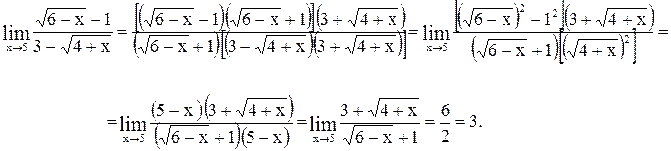
Контрольные варианты к задаче 3

Вычислить пределы функций:

1.	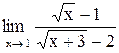.	2.	.	3.	.
4.	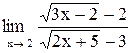.	5.	.	6.	.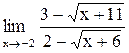
7.	.	8.	.	9.	.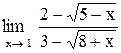
10.	.	11.	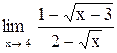.	12.	.
13.	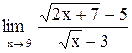.	14.	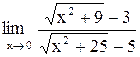.	15.	.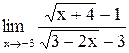
16.	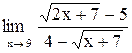.	17.	.	18.	.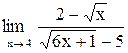
19.	.	20.	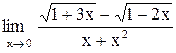.	21.	.
22.	.	23.	.	24.	.
25.	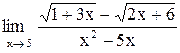.	26.	.	27.	.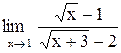
28.	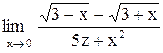.	29.	.	30.	.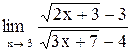

З а д а ч а 4

Если пр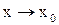и и, то отношение 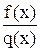представляет собой неопределенность . В этом случае рекомендуется числитель и знаменатель разделить почленно на старшую степень переменной х.

Пример 4

Вычислить предел .

.

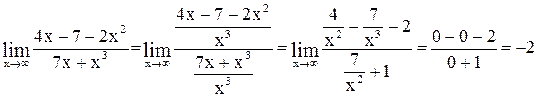Контрольные варианты к задаче 4

 

Вычислить пределы функций:

.	.
.	.
.	.
.	.
.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
	.
	.

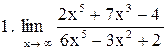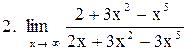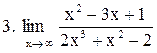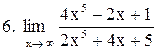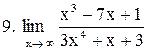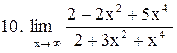
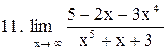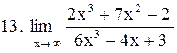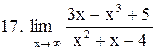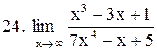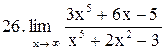З а д а ч а 5

 

Если при и , то разность представляет собой неопределенность . Чтобы раскрыть такую неопределенность, надо привести её к виду 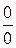или .

Пример 5

Вычислить предел .

Умножим и разделим на сопряженное выражение , тогда

 

Здесь старшая степень 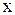- первая, поэтому

 

 

Контрольные варианты к задаче 5

Вычислить пределы функции:

.	.
.	.
.	.
.	.
.	.
.
.	.
.	.
.	.
.	.
	.
	.
.	.
.	.
.	.

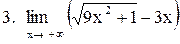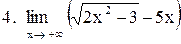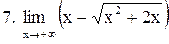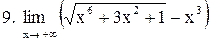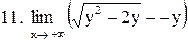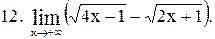
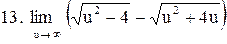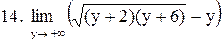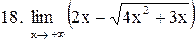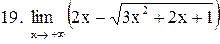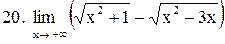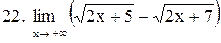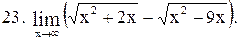
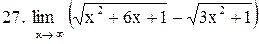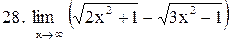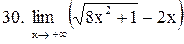З а д а ч а 6

Таким образом, если , то ~ .   Таблица эквивалентных бесконечно малых функций

Пример 6

Вычислить предел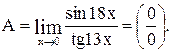

 

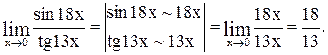
Пример 7

Вычислить предел

 

 

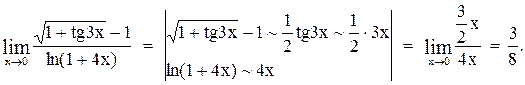
Пример 8

Вычислить предел

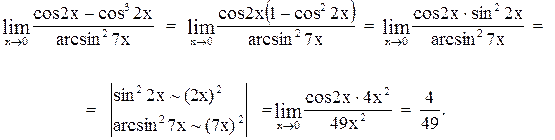
Контрольные варианты к задаче 6

 

Вычислить пределы функций:

 

.	.
	.
.	.
.	.
	.
.	.
.	.
.	.
.	.
	.
.	.
	.
.	.
.	.
.	.

 

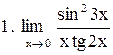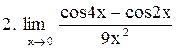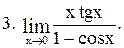
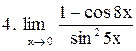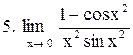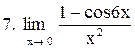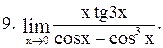
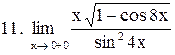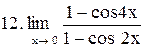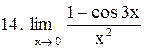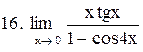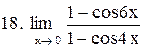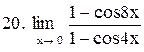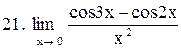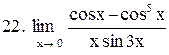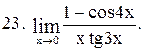
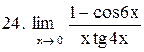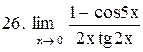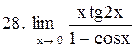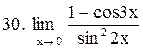З а д а ч а 7

Пример 9

Вычислить предел

 

 

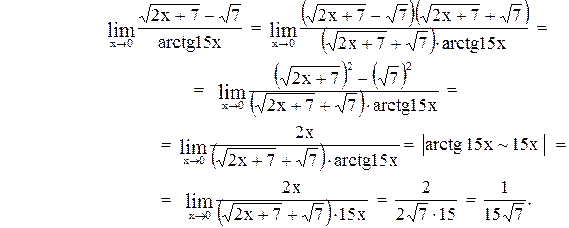
Контрольные варианты к задаче 7

Вычислить пределы функций:

	.
.	.
	.
.
	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.

 

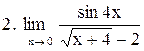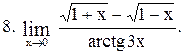
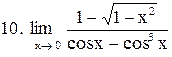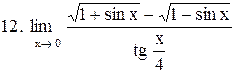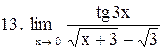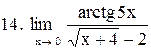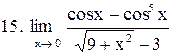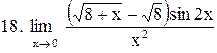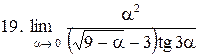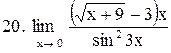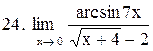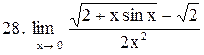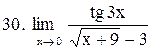З а д а ч а 8

  1. или 2.

Пример 10

Вычислить предел .

Здесь 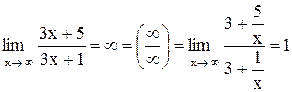,поэтому получим неопределенность

вида . Используем первую форму второго замечательного предела. Для этого преобразуем основание к виду следующим образом:

.

Тогда

,

т. к. , а предел основания равен е.

 

Контрольные варианты к задаче 8

Вычислить пределы функций:

1.	.	2.	.
3.	.	4.	.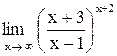
5.	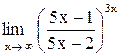.	6.	.
7.	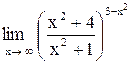.	8.	.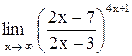
9.	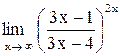.	10.	.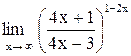
11.	.	12.	.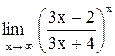
13.	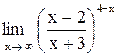.	14.	.
15.	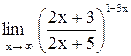.	16.	.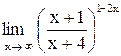
17.	.	18.	.
19.	.	20.	.
21.	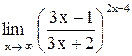.	22.	.
23.	.	24.	.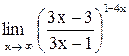
25.	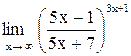.	26.	.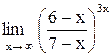
27.	.	28.	.
29.	.	30.	.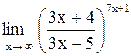

З а д а ч а 9

Пример 11

Вычислить 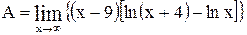. Это неопределенность вида .

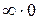Так как .

 

Найдем, используя свойство непрерывности логарифмической функции:

 

 

 

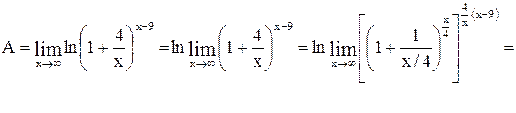
Контрольные варианты к задаче 9

Вычислить пределы функции:

 

1. .	2. .
3. .	4. .
5. 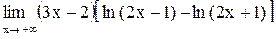.	6. .
7. .	8. .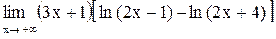
9. .	10. .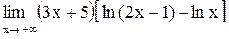
11. .	12. .
13. 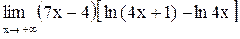.	14. .
15. .	16. .
17. 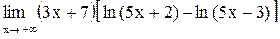.	18. .
19. .	20. .
21. .	22. .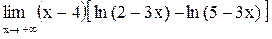
23. .	24. .
25. 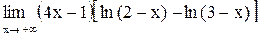.	26. .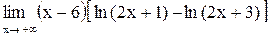
27. 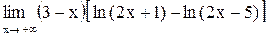.	28. .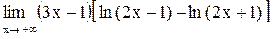
29. .	30. .

 

З а д а ч а 10

Пример 12

.

 

При подстановке предельного значения аргумента возникает неопределенность . Приведение к общему знаменателю сводит эту неопределенность к

неопределенност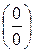и или .

.

 

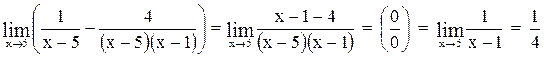Контрольные варианты задачи 10

Вычислить пределы функций:

 

.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
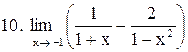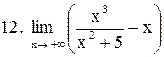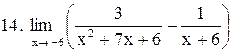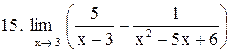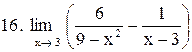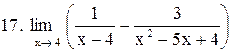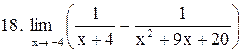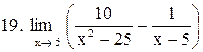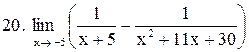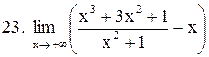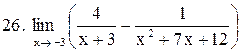27..	.
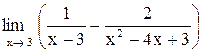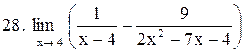29..	.

 

З а д а ч а 11

1) функция определена в этой точке и ее окрестности; 2) существует предел функции в точке , т. е. ; 3) предел функции в точке равен значению функции в этой точке.

Пример 13

Исследовать функцию на непрерывность. В точках разрыва установить характер разрыва. Схематично построить график функции

 

 

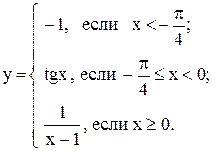
Функция задана тремя аналитическими выражениями, представляющими собой элементарные функции, которые непрерывны во всех точках, где они определены.

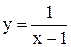Функция всюду определена, функция определена на промежутке , функция не определена в точке , которая является точкой разрыва. Точками разрыва могут быть также точки , где происходит смена аналитического выражения функции.

Исследуем на непрерывность функцию в точке .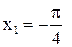

1. .

2. .

, .

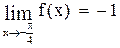3. .

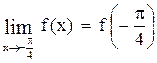В точке функция непрерывна.

Исследуем на непрерывность функцию в точке .

1. .

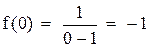2. , .

 

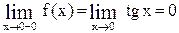Так как односторонние пределы в точке 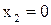не равны между собой, предел функции в точке 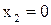не существует. Однако односторонние пределы в этой точке существуют и конечны, поэтому - точка неустранимого разрыва I рода.

Определим характер разрыва функции в точке .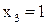

 

.

.

 

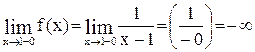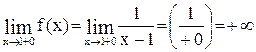Так как односторонние пределы функции в точке бесконечны, точка - точка разрыва второго рода.

График функции, имеет следующий вид.

Исследовать функцию на непрерывность. В точках разрыва установить характер разрыва. Схематично построить график функции:

 

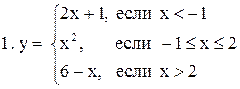
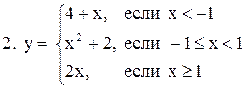
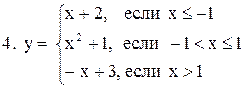
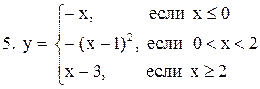
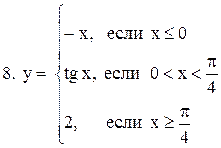
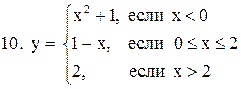
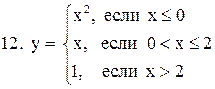
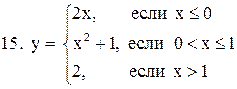
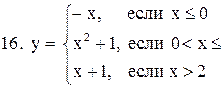
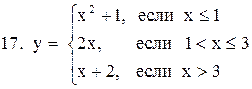
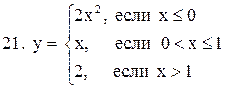
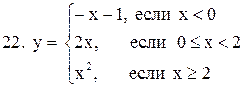
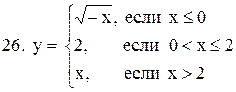
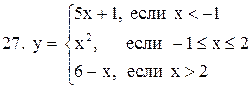
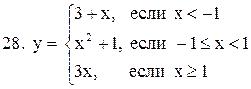
З а д а ч а 12

Известно, если .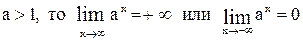

Пример 14

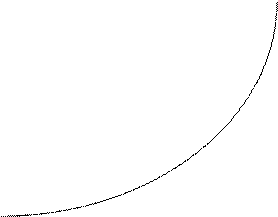
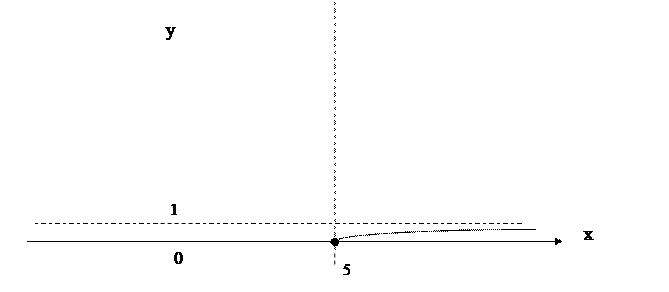
Исследовать функцию 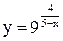на непрерывность. Установить характер точек разрыва. Схематично построить график функции .

Функция 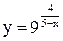элементарная, поэтому она непрерывна во всех точках, кроме точки 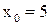, где она не определена.

, .

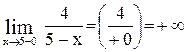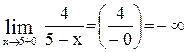Поэтому , 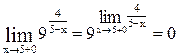. В точке - разрыв II рода, т. к. левосторонний предел бесконечен.

 

Контрольные варианты задачи 12

 

Исследовать функцию на непрерывность. В точках разрыва установить характер разрыва. Схематично построить график функции:

 

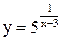
1.	2.	3.	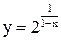4.	5.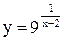
6.	7.	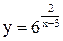8.	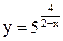9.	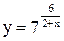10.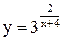
11.	12.	13.	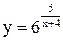14.	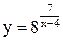15.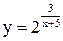
16.	17.	18.	19.	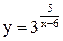20.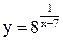
21.	22.	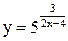23.	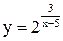24.	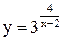25.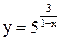
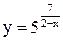
26.	27.	28.	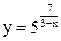29.	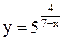30.

 

 

З а д а ч а 13

По определению модуль числа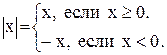

 

Следовательно,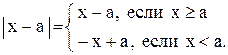

 

 

Пример 15

 

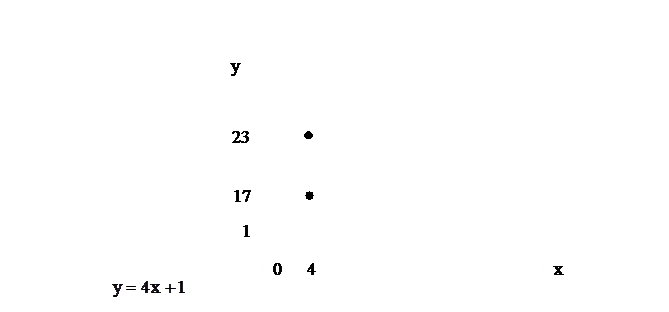
Исследовать функцию на непрерывность. Установить характер разрыва. Построить график функции

 

.

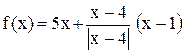так как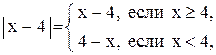

 

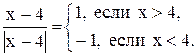
Функция 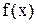не определена в точке 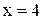. Эта функция может быть записана в виде

 

Каждое из аналитических выражений непрерывно, следовательно, функция 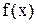имеет разрыв только в точке , где она не определена. Слева от этой точки

функция задана формулой 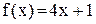. Следовательно, =

. Справа от точки функция задана формулой 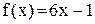, поэтому . Односторонние пределы в точке конечны, но не равны между собой. Предел функции в точке не существует. Функция имеет разрыв в этой точке, который является неустранимым разрывом I рода (скачком).

 

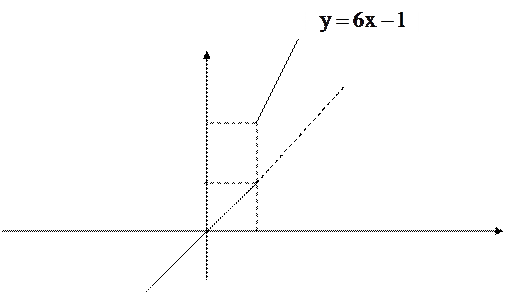
Контрольные варианты задачи 13

 

Исследовать функцию на непрерывность. В точках разрыва установить характер разрыва. Схематично построить график функции:

 

.	.
.	.
.	.
.	.
.	.
	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.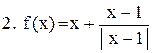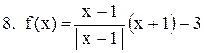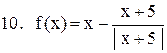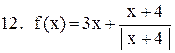
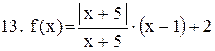
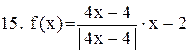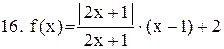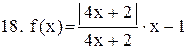
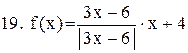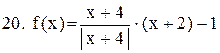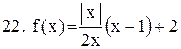
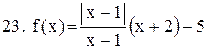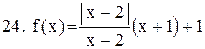
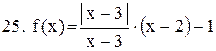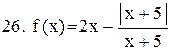
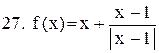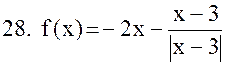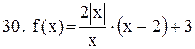