Леммы Чебышева.

В этом пункте докажем следующие две леммы, принадлежащие Чебышеву*

Лемма 1. Пусть 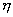— случайная величина, принимающая только неотрицательные значения; тогда

Доказательство:

Для простоты докажем это утверждение для дискретной случайной величины 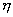, принимающей значения x₁, x₂, ..., x_n, при условии 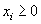. По аксиоме сложения вероятностей имеем

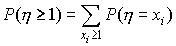
где суммирование распространено на все значения x_i, большие или равные единице. Но для sub>, очевидно,

Поэтому

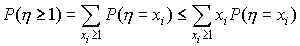
(50)

где x_i<1. Эта сумма неотрицательна, так как все 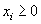по условию, а вероятности 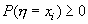. Поэтому

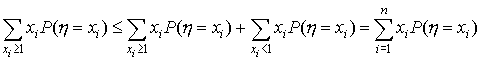
(51)

Последняя сумма распространена на все значения x_i, принимаемые учайной ветчиной 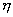. Но эта сумма по определению равна математическому ожиданию:

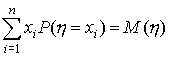
Сопоставляя соотношения (50) и (51), имеем

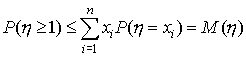
Тем самым лемма доказана.

 

Лемма 2. Пусть 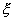— случайная величина, а 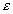- положительное число. Тогда вероятность того, что модуль отклонения случайной величины. 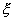от ее математического ожидания окажется меньше, чем 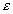, больше или равна разности

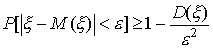
(52)

Неравенство (52) называется неравенством Чебышева.

 

Доказательство:

Рассмотрим сначала неравенство 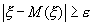. Так как оно равносильно неравенству

то

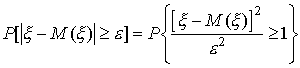
Случайная величина

неотрицательна и, значит, удовлетворяет условиям первой леммы Чебышева. Следовательно,

так как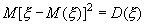

Поэтому

(53)

 

Так как событие, выражаемое неравенством 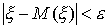, противоположно событию, выражаемому неравенством 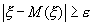, то

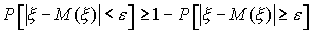
Принимая во внимание соотношение (53), окончательно получим

 

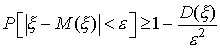
* П.Л.Чебышев (1821-1894) - выдающийся русский математик.