Определение неизвестных параметров распределения.

C помощью гистограммы мы можем приближенно построить график плотности распределения случайной величины 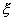. Вид этого графика часто позволяет высказать предположение о плотности распределения вероятностей 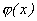случайной величины 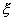. В выражение этой плотности распределения обычно входят некоторые параметры, которые требуется определить из опытных данных.
Остановимся на том частном случае, когда плотность распределения 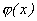зависит от двух параметров.
Итак, пусть x₁, x₂, ..., x_n - наблюдаемые значения непрерывной случайной величины 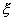, и пусть ее плотность распределения вероятностей зависит от двух неизвестных параметров A и B, т.е. имеет вид 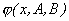. Один из методов нахождения неизвестных параметров A и B состоит в том, что их выбирают таким образом, чтобы математическое ожидание и дисперсия теоретического распределения совпали с выборочными средними значением 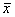и дисперсией :

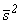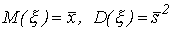
(66)

где

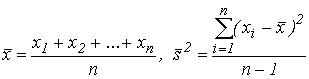
(67)

Из двух полученных уравнений (66) находят неизвестные параметры A и B. Так, например, если случайная величина 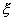подчиняется нормальному закону распределения вероятностей, то ее плотность распределения вероятностей

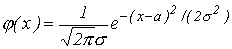
зависит от двух параметров a и 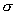. Эти параметры, как мы знаем, являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины 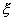; поэтому равенства (66) запишутся так:

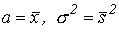
(68)

Следовательно, плотность распределения вероятностей имеет вид

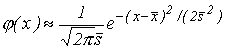
Замечание 1. Такую задачу мы уже решали в § 7. Результат замера есть случайная величина 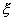, подчиняющаяся нормальному закону распределения с параметрами a и 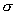. За приближенное значение a мы выбрали величину 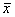, а за приближенное значение 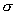- величину .

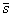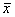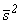Замечание 2. При большом количестве опытов нахождение величин и по формулам (67) cвязано с громоздкими вычислениями. Поэтому поступают так: каждое из наблюдаемых значений величины 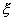, попавшее в i-й интервал ] X_i-1, X_i [ статистического ряда, считают приближенно равным середине c_i этого интервала, т.е. c_i=(X_i-1+X_i)/2. Рассмотрим первый интервал ] X₀, X₁ [. В него попало m₁наблюдаемых значений случайной величины 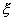, каждое из которых мы заменяем числом с₁. Следовательно, сумма этих значений приближенно равна m₁с₁. Аналогично, сумма значений 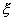, попавших во второй интервал, приближенно равна m₂с₂ и т.д. Поэтому

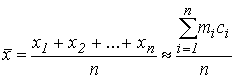
Подобным же образом получим приближенное равенство

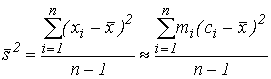
Итак,

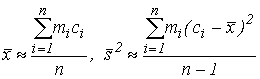
(69)

где n=m₁+m₂+...+m_k, а k - число интервалов статистического ряда.

Замечание 3. На практике для еще большего упрощения вычислений прибегают к следующему приему. Пусть x₀ - произвольное число. Обозначим u_i=с_i-x₀ и рассмотрим величины v₁ и v₂, определяемые соотношениями

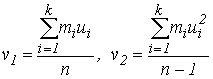
(70)

Покажем, что

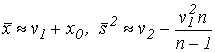
(71)

Действительно,

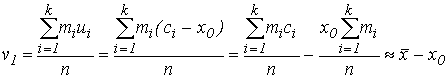
так как

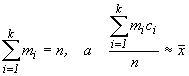[cм.формулы (69)].

Итак, 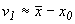, откуда 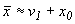. Аналогично доказывается и второе из соотношений (71)

Пример. Построенная гистограмма для статистического распределения значений диаметра вала хвостовика (см. рис. 17) позволяет сделать предположение о том, что мы имеем дело с нормальным законом распределения. Требуется, исходя из опытных данных, представленных в таблице из примера п.8.1., определить параметры a и 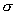этого распределения.

Решение. Полагая* x₀=75, вычислим v₁ и v₂. Вычисления расположим, как указано в следующей таблице.

Номера интервалов	Cередина интервала c_i	m_i	u_i=с_i-75	m_iu_i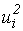
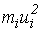
			-8	-32
			-6	-72
			-4	-96
			-2	-82

По формулам (70) находим

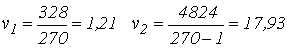
Используя теперь формулы (71), имеем

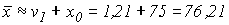
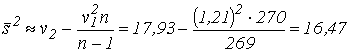
Выберем параметры a и 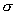так, чтобы выполнялись условия (68): 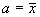, 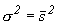. Следовательно, 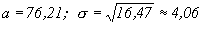. Таким образом, плотность распределения вероятностей

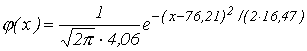
В следующей таблице приведены вычисления значений функции 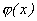в средних точках интервала статистического ряда. Значения функции 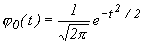взяты из Табл. I Приложения.

x	x-76,21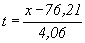
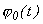
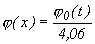
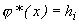
	-9,21	-2,27	0,0303	0,006	0,008
	-7,21	-1,78	0,0818	0,020	0,022
	-5,21	-1,29	0,1736	0,043	0,045
	-3,21	-0,79	0,2920	0,072	0,076
	-1,21	-0,30	0,3697	0,091	0,092
	0,79	0,20	0,3825	0,095	0,098
	2,79	0,69	0,3144	0,075	0,072
	4,79	1,18	0,1989	0,049	0,048
	6,79	1,62	0,0973	0,024	0,024
	8,79	2,17	0,0379	0,009	0,009
	10,79	2,66	0,0116	0,003	0,004
	12,79	3,16	0,0020	0,001	0,002

В последнем столбце таблицы приведены значения функции 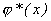, взятые из столбца (5) таблицы из примера из п.8.1. Сравнение показывает, что функция 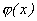близка к .

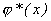* Для простоты вычислений, как это обычно делается, за x₀ мы выбрали число, близкое к середине диапазона изменения наблюдаемых значений.

§ 9. ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИЙ.

1. Введение.

В математическом анализе мы имеем дело с функциональной зависимостью между двумя переменными величинами, при которой каждому значени. одной их них соответствует единственное значение другой.
Однако часто приходится иметь дело с более сложной зависимостью, чем функциональная. Такая зависимость возникает тогда, когда одна из величин зависит не только от другой, но и от ряда прочих меняющихся факторов, среди которых могут быть и общие для обеих величин.
Так, например, с увеличением высоты сосны увеличивается диаметр ее ствола. Однако если исследовать эту зависимость по опытным данным, то может оказаться что для отдельных сосен с большей высотой диаметр ствола окажется меньше, чем для сосен с меньшей высотой. Это объясняется тем, что диаметр ствола сосны зависит не только от ее высоты, но и от других факторов (например, от свойств почвы, количества влаги и т.д.).
Это обстоятельство наглядно видно из таблицы, в которой приведены значения диаметров ствола сосны в зависимости от ее высоты. В каждой клетке этой таблицы помещено число сосен, имеющих соответствующие диаметр ствола и высоту*. Так, например, количество сосен с высотой 24 м и с диаметром ствола 26 см равно двум.

	Высота (в м)
Диаметр (в cм)	22,5-23,5 23	23,5-24,5 24	24,5-25,5 25	25,5-26,5 26	26,5-27,5 27	27,5-28,5 28
20-24 22
24-28 26
28-32 30
32-36 34
36-40 38
40-44 42
44-48 46

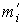
Ниже приведены средние значения диаметра ствола сосны в зависимости от высоты.

Высота
Средний диаметр				34,7	39,6

Мы видим, что с увеличением высоты сосны в среднем растет диаметр ее ствола. Однако сосны заданной высоты имеют распределение диаметров с довольно большим рассеянием. Если в среднем, например, 26-метровые сосны толще, чем 25-метровые, то для отдельных сосен это соотношение нарушается.
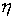В рассмотренном примере мы имеем две случайные величины: - высота сосны и - диаметр ее ствола. Каждому значению xвеличины соответствует множество значений 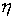, которые она может принимать с различными вероятностями. Говорят, что между и 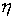существует корреляционная зависимость.
Этот пример приводит нас к следующему определению.
Две случайные величины и 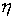находятся в корреляционной зависимости, если каждому значению одной из этих величин соответствует определенное распределение вероятностей другой.
Для характеристики корреляционной зависимости между случайными величинами вводится понятие коэффициента корреляции.

* При подсчетах мы принимаем диаметры стволов и высоты всех сосен, попавших в данный интервал, равными серединам соответствующих интервалов.