BİR PARÇACIĞIN YÖRÜNGESİ VE UZAY-ZAMANDAKİ DURUMU
Sırası gelmişken burada biraz da kuantum mekaniğinden bahsetmek istiyorum. Klasik düzeyde tek bir kuantum parçacığını düşünürsek, parçacık uzaydaki konumu ile tanımlanır ve bir sonraki evredeki davranışını bilmek için hızını (veya eşdeğer olarak Momentumunu) bilmeliyiz. Kuantum mekaniksel açıdan, bir parçacığın bulunabileceği her bir konum, ona sunulan bir seçenektir. Bu seçenekler, olasılık dağılım fonksiyonlarıyla ifade edilip daha sonra da çarpılıp toplanabilirler. Kuantum kuramında, konumun bir kompleks değerli fonksiyonu olarak kabul edilen ve parçacığın Dalga Fonksiyonu denilen bu fonksiyon ψ ile gösterilir ve herhangi bir x konumu için, dalga fonksiyonu, ψ(x) değerine sahiptir ve bu parçacığın x konumunda bulunması olasılığının genliğidir.
Kompleks değerli ψ, üç boyutlu uzayda parçacığın x-ekseni boyunca hareket ettiğini varsayarsak, y-yönünün de reel ekseni oluşturduğunu düşünürsek; z-yönü sanal eksen olur. Yani x-eksenindeki her konuma karşı (y,z) düzleminde bir nokta işaretleyebiliriz. x değiştikçe bu nokta da değişir ve izlediği yol x-ekseninin yakın komşuluğu içinde dolanarak uzayda bir eğriyi tanımlar. Bu eğriye, parçacığın ψ eğrisi denir. Parçacığın belirli bir x noktasında bulunma olasılığı, bu noktaya bir parçacık dedektörü yerleştirilmiş gibi düşünürsek, ψ(x) genlik değerinin mutlak değerinin karesini alarak bulunabilir:
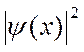
Bu ifade, ψ-eğrisinin x-ekseninden uzaklığının karesidir. Bu durumu, üç boyutlu fiziksel uzaydaki bir dalga fonksiyonu ile ifade etmek için, üç boyutu fiziksel uzaya ve iki boyutu ψ(x)in işaretlendiği her noktadaki konumu belirten düzleme karşılık gelmek üzere beş boyut gerekir. Bu durumda 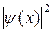 ifadesi bir olasılık yoğunluğunu belirtir. Bunun olasılık yoğunluğu ise, bir noktanın komşuluğundaki sabit uzunlukta küçük bir aralıkta parçacığın bulunması olasılığıdır. Böylece ψ(x), bir genlikten çok bir genlik yoğunluğunu tanımlar.
ifadesi bir olasılık yoğunluğunu belirtir. Bunun olasılık yoğunluğu ise, bir noktanın komşuluğundaki sabit uzunlukta küçük bir aralıkta parçacığın bulunması olasılığıdır. Böylece ψ(x), bir genlikten çok bir genlik yoğunluğunu tanımlar.
Ψ Kompleks Dalga Fonksiyonu ifadesi:
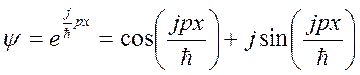
olarak ifade edilebilir. Buradaki p parçacığın söz konusu momentumudur. Bu dalga fonksiyonu ifadesi ise, ψ-eğrisi olarak matematiksel olarak bir helezonu tanımlamaktadır. Helisin genliği pye bağlıdır ve büyük Momentumlar sık helezonlara; küçük Momentumlar seyrek helezonlara karşılık gelmektedir.
Sırası gelmişken, teorimizde sıkça kullandığımız ve Kütleçekim alanının da helezonik bir şekilde olması sebebiyle, burada bu helezonik yapının matematiksel yapısını biraz açabiliriz. a helezonun yapıçapı ve b helezonun sıklığını gösteren katsayılar olmak üzere bir helezonun kartezyen koordinatlardaki genel olarak parametrik denklemi;
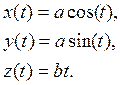
denklemleriyle ifade edilebilir. Helezonu tanımlamanın bir diğer kullanışlı yolu da, eix şeklinde Euler açılımıyla komplex-polar koordinat sisteminde göstermektir;
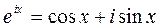
Özel olarak, kütleçekim alanında helezonik yüzey üzerindeki diferansiyel uzaklık ifadesinde kullanılan koordinat şekli ELİPSOİDAL HELEZON olup;
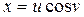 ,
, 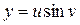 ve
ve 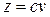 veya hiperbolik formda;
veya hiperbolik formda;

olmak üzere 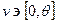 ve
ve  aralığında integrali alınırsa;
aralığında integrali alınırsa;
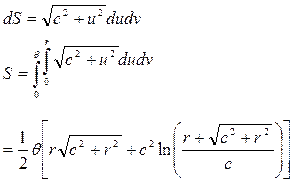
ve elipsoidal helezonun yüzey eğriliği;
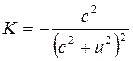
olarak belirlenir. Bu durumda bu metrik uzaklık ifadesi, minkowsky uzayında c, ışık hızında titreşen bir elipsaidal helezon yüzeyi tanımlar. Eğer, küresel koordinat sisteminde helezonu parametrik olarak tanımlarsak ve 4-boyutlu uzay-zaman için diferansiyel uzaklık ifadesini yazarsak;
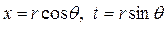 olmak üzere;
olmak üzere;

ve uzaya yayılan ekstra 5. boyutu da  olarak eklersek, 5-boyutlu helezonik diferansiyel uzaklık ifadesi;
olarak eklersek, 5-boyutlu helezonik diferansiyel uzaklık ifadesi;

şeklinde olur.
Türk fizikçisi Prof. Ergin SEZGİNe göre, bu helezonik yüzey 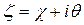 olmak üzere,
olmak üzere, 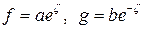 şeklinde değişen iki HOLOMORFİK parametrik denklemle yeniden belirlenirse 3lü grup simetrisine sahip SU(3) ve SO(3) grup simetrisine sahip bir sicim manifoldunun hiperyüzeyine denk gelebilir. Hatırlarsak, uzay-zaman yapısının HİPERBOLOİD yapısını göz önüne alarak, birleşik alan teorisinde Conform dönüşümü kullanmıştık. Teorimizde kullanmayacağımız için, holomorfik uzay dönüşümlerinin detaylarına girmedik. Geometrik olarak gösterimi zor olan bu dönüşüm sonucunda bir geometrik şekil, sicimlerin 5-boyutlu ek uzay-zaman boyutlarına yayılması sonucu ELİPTİK HELEZONOİD bir kıvrım yüzeyi oluşturduğunu öngörür.
şeklinde değişen iki HOLOMORFİK parametrik denklemle yeniden belirlenirse 3lü grup simetrisine sahip SU(3) ve SO(3) grup simetrisine sahip bir sicim manifoldunun hiperyüzeyine denk gelebilir. Hatırlarsak, uzay-zaman yapısının HİPERBOLOİD yapısını göz önüne alarak, birleşik alan teorisinde Conform dönüşümü kullanmıştık. Teorimizde kullanmayacağımız için, holomorfik uzay dönüşümlerinin detaylarına girmedik. Geometrik olarak gösterimi zor olan bu dönüşüm sonucunda bir geometrik şekil, sicimlerin 5-boyutlu ek uzay-zaman boyutlarına yayılması sonucu ELİPTİK HELEZONOİD bir kıvrım yüzeyi oluşturduğunu öngörür.
Bu durumda, bu metrik izotropik uzay-zaman manifoldunun yüzeyi kompleks düzlemde;
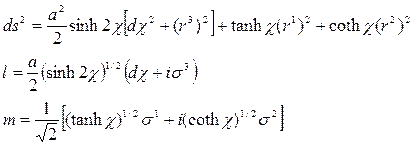
şeklinde düz ve eğri uzay-zaman bileşenlerinden oluşan iki parçalı bir yapı sunar.
Aşağıdaki şekillerde bu manifold yüzeylerine ait çeşitli modeller verilmektedir:
