Yüzey ve Hacim İntegralleri

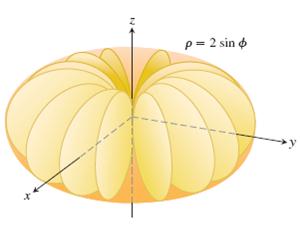
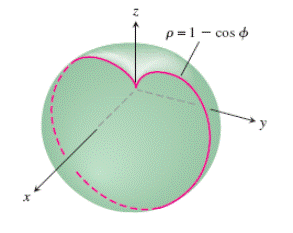
Bazı fonksiyonların yüzey integralleri bildiğimiz nesnelere benzeyen şekiller verir. Bir örnek: Lemniskat 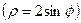 ve Kardioid (Kalp) eğrisinin
ve Kardioid (Kalp) eğrisinin 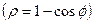 kendi ekseni etrafında döndürülmesi Kabak ve Elma şekillerini meydana getirir. İlginçtir ki, -Newtonun başına düşen!- elmanın şeklini belirleyen yüzey alanı, katı bir cismin eylemsizlik momentine ilişkin üç katlı hacim integraline denk gelir.
kendi ekseni etrafında döndürülmesi Kabak ve Elma şekillerini meydana getirir. İlginçtir ki, -Newtonun başına düşen!- elmanın şeklini belirleyen yüzey alanı, katı bir cismin eylemsizlik momentine ilişkin üç katlı hacim integraline denk gelir.
 vektör alanını ve şekilde görülen S yüzeyini göz önüne alalım. S yüzeyini dS1, dS2, ..., dSn gibi küçük parçalara ayıralım. Her bir yüzey parçasının bulunduğu yerde
vektör alanını ve şekilde görülen S yüzeyini göz önüne alalım. S yüzeyini dS1, dS2, ..., dSn gibi küçük parçalara ayıralım. Her bir yüzey parçasının bulunduğu yerde  vektör alanının ortalama değerini
vektör alanının ortalama değerini  1,
1, 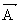 2, ...
2, ... 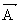 n ile gösterilim ve her bir dSk yüzeyinde dik birim vektör
n ile gösterilim ve her bir dSk yüzeyinde dik birim vektör  , dSk nın dışına doğru pozitif alınır.
, dSk nın dışına doğru pozitif alınır.
 vektör alanının S yüzeyi üzerindeki akışlı toplamını hesaplar ve dSi ® D limitini alırsak yüzey integrali kavramına ulaşırız:
vektör alanının S yüzeyi üzerindeki akışlı toplamını hesaplar ve dSi ® D limitini alırsak yüzey integrali kavramına ulaşırız:

Genel olarak sonsuz küçük yüzey elemanı
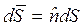
olarak tanımlanır, böylece yüzey integrali,
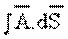
şeklinde yazılır ve S yüzeyi kapalı bir yüzey ise,

şeklinde gösterilir, burada 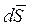 her yerde yüzeyin içinden dışına doğru yöneltilmiştir. Böyle bir integrali hesaplayabilmek için
her yerde yüzeyin içinden dışına doğru yöneltilmiştir. Böyle bir integrali hesaplayabilmek için 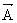 ve
ve 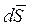 yi açık fonksiyonel formda ifade edebilmeliyiz. İki değişken üzerinden hesaplanan integrallere çift hatlı integraller adı verilir. Genel olarak,
yi açık fonksiyonel formda ifade edebilmeliyiz. İki değişken üzerinden hesaplanan integrallere çift hatlı integraller adı verilir. Genel olarak, 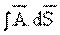 : Anın S yüzeyi üzerinden akışını ifade eden çift katlı integraldir.
: Anın S yüzeyi üzerinden akışını ifade eden çift katlı integraldir.
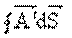 ,
, 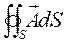 olarak kapalı yüzey boyunca yüzey integrali (Çift katlı integral)
olarak kapalı yüzey boyunca yüzey integrali (Çift katlı integral)
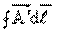 ,
,  olarak kapalı yol boyunca çizgi integrali (Tek katlı integral)
olarak kapalı yol boyunca çizgi integrali (Tek katlı integral)
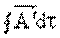 ,
, 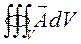 olarak kapalı hacim boyunca hacim integrali (Üç katlı integral) olarak tanımlanır.
olarak kapalı hacim boyunca hacim integrali (Üç katlı integral) olarak tanımlanır.
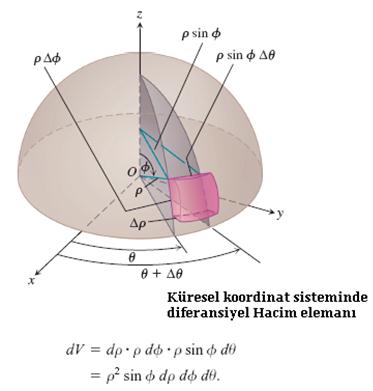
Hacim integralinde dt uzayın V gibi bir kapalı bölgesinde tanımlanan sonsuz küçük bir diferansiyel hacim elemanıdır (Örneğin, Kartezyen koordinatlarda dt= dx.dy.dzdir). Hacim integralleri, üç katlı integrallerdir ve Birleşik alan teorisinde yük veya kütle yoğunluklarının hesaplanmasında kullanılırlar.