Gradient

f(x, y, z) bir skaler alan olsun ve (x, y, z) noktasından sonsuz k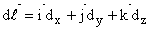ьзьk vektцr, olmak ьzere eğri ьzerinde df kadar ayrıldığımızda f(x, y, z)’nin nasıl değiştiğin bilmek istediğimizi dьşьnelim. Temel analiz kuramına gцre,

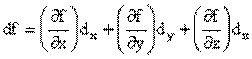
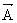olduğunu biliyoruz. df ifadesinin d ile belli bir vektцrьnьn skaler зarpım olarak yazabiliriz, df = .d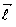Yukarıdaki iki df bağıntısını kıyaslarsak,

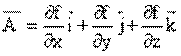
olduğunu gцrьrьz. Fonksiyonun herhangi bir aralıkta artış veya azalış gцsterip gцstermemesine gцre Gradyan herhangi bir noktada pozitif veya negatif olabilir.

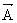vektцrьnde “f’nin gradienti “ adı verilir ve gradient operat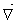цrь (veya “del”)

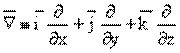
şeklinde tanımlanmak ьzere 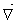f şeklinde yazılır. Bu durumda, df diferansiyeli;

df = f.d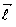

olarak yazılır, buradan 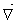f ’nin, bьyьklьk ve doğrultusu f’nin en bьyьk uzaysal değişim hızına eşit olan bir vektцr olduğunu gцrьrьz. Bu yьzden 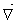f, f‘nin daha bьyьk değerlerine doğru yцnelmiş bir vektцr operatцrьnь tanımlamaktadır.

Bazı gradient цzdeşlikleri:

Diverjans Teoremi (Gauss Yasası)

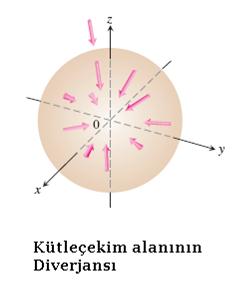
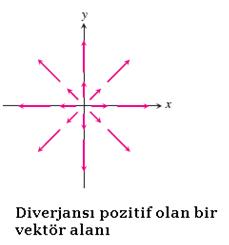
Aşağıdaki şekilde, 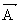vektцr alanının S yьzeyi ьzerinden akısının,

 

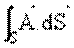
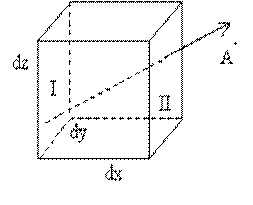
olarak hesaplanacağını dьşьnьrsek, akının hesabı iзin aşağıda gцsterilecek değişik bir yцntem daha vardır. (x, y, z) noktasını iзine alacak şekilde yerleştirilmiş dx, dy, dz sonsuz kьзьk hacim elemanını gцz цnьne alalım. 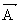alanının bileşenlerinin x, y, z koordinatlarının fonksiyonları olarak belirlendiklerini varsayalım ve I ve II yьzeyleri boyunca 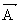‘nın akısının hesaplayalım. Sağ yьz ьzerinde A_x ьз değeri bu yьz ьzerindeki ortalama değerdir, bцylece dışarı doğru akı,

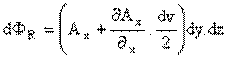
sol yьzdeki akı iзeri doğrudur:

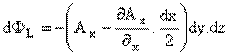
bцylece bu iki yьzden geзen toplam dışarı doğru akı (¶A_x/¶_x) dx.xy.dz ‘ye eşit olur. benzer şekilde kьpьn diğer yьzleri ьzerinden geзen toplam dışarı doğru akıları hesaplar ve toplarsak,

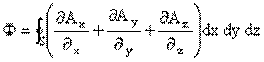
buluruz. Sonsuz kьзьk hacim elemanı iзinde,

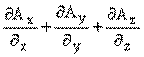
bьyьklьğь, birim hacim başına dışarı doğru toplam akıyı verir ve (x, y, z) noktasında 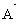vektцr alanının diverjansı adını alır. Bu bьyьklьk div 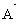olarak veya 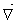operatцrь kullanılarak,

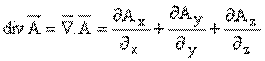
skaler olarak yazılmış olur. Bu vektцr alanının diverjansı skaler bir bьyьklьktьr. Bu hesaba sonsuz kьзьk hacim elemanından sonlu bir hacme genellemek iзin, sonlu hacmi sonsuz kьзьk hacim elemanlarına bцlmek ve bunlar ьzerinde toplam almak gerekir. Birbirlerine bitişik yьzeylerde bir hacim elemanı iзin bu akı değerinin bir parзası dışarı doğru; diğer iзin ise, iзeri doğru olur ve bьtьn hacim ьzerinden alınan toplamda bu katkılar birbirlerini yok edeceklerinden yalnızca dış yьzey ьzerinden dışarı doğru akı elde edilir ve sonuз,

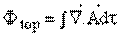
olarak bulunur. Yukarıda verilen akı tanımı ile;

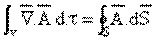
yazılabilir. Bu eşitlik “Diverjans Teoremi”nin ifadesidir. Eşitliğin sağ yanındaki integral, kapalı S yьzeyi boyunca; soldaki hacim integrali ise, S ile sınırlı hacim ьzerinden alınacaktır.