Eğri Uzay-Zaman

Цklit Geometrisinde iki nokta arasındaki en kısa yolun doğru olduğunu цğrenmişizdir. Burada en kısa yol deyimi uzaklık kavramıyla ilgilidir. Цklit geometrisinde uzaklık bir metrik (fonksiyon) ile tanımlanır. P(x₁,y₁,z₁) ile Q(x₂,y₂,z₂) noktaları arasındaki uzaklık (metrik) olarak;

bağıntısıyla verilir. Bilindiği gibi bu metrik katı dцnьşьmler altında değişmez. Katı dцnьşьm deyiminden цteleme (paralel kayma) ve dцnme dцnьşьmlerini anlıyoruz. Katı dцnьşьmler uzunluğu ve aзıyı değiştirmez. Цklit geometrisinde geзerli olan bu kurallar başka geometrilerde başka biзimlere girebilir. Цrneğin, Lizbon’dan New York’a gidecek gemi ya da uзak, en kısa yoldan gitmek isterse, iki kentten geзen paralel daireyi izlemez. Kaptanlar bu iki kentten geзen bьyьk зember ьzerinde giderler. Bu nedenle, yolcular цnce kuzeye doğru зıkıldığı sonra gьneye doğru inildiği izlenimini edinirler. Зьnkь, kьre ьzerindeki P noktasından bir Q noktasına giden en kısa yol P ve Q dan geзen bьyьk зember yayıdır. Цklit uzayındaki 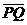doğrusunun yerini k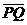ьrede bьyьk зember yayı almıştır (Şekil-I). Başka yьzeylerde başka biзimler alacaktır. Цrneğin, silindir yьzeyinde başka, hiperboloid yьzeyinde başkadır. Gцrelilikte kullanılan terimlere uyum sağlamak iзin, Цklit uzayına dьz uzay –flat space- , Цklit dışı uzaylara da eğri uzay –curved space- denir.

 

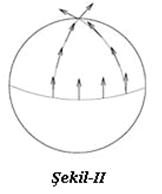
Цklit uzayında bir vektцrь, kendisine paralel olarak, kapalı bir eğri boyunca kaydırarak (цteleme) ilk noktaya kadar getirdiğimizde, vektцrьn orijinal vektцrle зakıştığını gцrьrьz. Fakat, kьre ьzerinde bu цzellik kaybolur. Başka bir deyişle, kьre ьzerinde paralel kayma yola bağlı olarak değişir (Şekil-II). Bu цzellikten yararlanarak, yьzeyin eğriliğini (curvature) hesaplarız (Şekil-III). Diferansiyel Geometri derslerinde, eğriliğin ikinci basamaktan tьrevle hesaplandığını anımsayınız. Цte yandan, fizik derslerinde, ivmenin de ikinci basamaktan tьrevle hesaplandığını gцrmьşsьnьzdьr. Buradan, ivme ile eğrilik arasında bir ilişki kurulabileceği sezilmektedir. Цte yandan, gravitasyonun ivmeye eşit olduğunu sцyledik. O halde, gravitasyon ile eğrilik arasında bir ilişki doğmaktadır. Bьtьn bu sцylediklerimizin matematiksel kanıtı vardır. Kanıtlarına ve teorik detaylarına giremeyeceğimiz Genel Gцrelilik Kuramının matematiği bunu yapmaktadır.

Uzay-zamanda her olay bir nokta ile gцsterilir. İşin iзine zaman girdiği iзin, uzay-zamanda iki nokta arasında Цklit geometrisindekine benzer bir uzaklıktan sцz edemeyiz. Bunun yerine, noktalar arasındaki uzaklık terimi yerine, iki olay arasındaki uzay-zaman aralığı terimi kullanılır. Buna gцre, Dt sьresi iзinde uzay koordinatlarındaki değişim Dx , Dy , Dz ise, uzay-zaman aralığı aşağıdaki bağıntı ile tanımlanır:

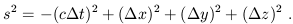
Bu bağıntı Minkowsky metriği diye bilinir. Цklit metriği negatif değer alamazdı ama Minkowsky metriği negatif ve pozitif değerler alabileceği gibi, farklı olaylar (noktalar) iзin sıfır değerini bile alabilir. Burada c bir dцnьşьm sabitidir ve pratikte onu ışık hızı olarak kabul edeceğiz. Bu metrikte цnemli olan şey, fotonların c hızıyla gitmesinden зok, koordinat dцnьşьmleri altında uzay-zaman aralığını değişmez kılan bir c sabitinin varlığıdır. Başka bir deyişle, (t,x,y,z) eylemsiz sisteminden (t’,x’,y’,z’) eylemsiz sistemine geзilirse aşağıdaki eşitliği sağlayan bir c sabiti vardır.

Matematikзiler, Minkowsky metriğini daha zarif yollarla tanımlamayı ve Gцrelilik Kuramını sağlam bir matematiksel yapı iзine almayı severler. Bu yцnde yapılanlar цğrenilmeye değecek zerafet ve зekiciliktedir. Halen aktif зalışma alanı olan Gauge Kuramı, String Kuramı, M kuramı gibi kuramlar, Einstein’in kullandığı tansцr yerine başka matematiksel yapılar koymaktadır. Aslında, matematiksel olarak bizim bu зalışmada ele aldığımız birleşik alan teorisi yaklaşımı da, bu зeşit bir farklı tansцr hesabı kurmaktan başka bir şey değildi. Bunların her birisi oldukзa geniş konular olup, bu ek bцlьme sığmayacak bьyьklьktedir. O nedenle, burada sadece işin matematiğini yapmak yerine, Einstein’in yaptıklarını betimlemekle yetinmek zorundayız.

Tansцr hesabında bir noktanın koordinatları alt indislerle değil ьst indislerle gцsterilir. İşlemlerde, bileşen sayıları onlarla sayılacak kadar зok olduğu iзin kısaltmalar kullanılır. Цrneğin, uzay-zamanda dцrt boyutlu bir noktayı (olayı) gцstermek iзin grek ьssь kullanılır. Zaman boyutunu dışlayıp uzaydaki ьз boyutu belirtmek istersek, grek ьssь değil, latin ьssь kullanılır:

Uzay-zaman aralığını daha kısa yazabilmek iзin, adına metrik denen,

matrisi kullanılır. Kьtleзekimi alanı iзin bu metrik, “g_μv, metrik birim tansцr” adını almaktadır. Einstein basitliği seven bir insandı. Зok sayıda indisli terimlerin toplamını yazmak iзin kolay bir kısaltma цnerdi. Aynı ьssь ya da indisi taşıyan terimler bьtьn mьmkьn haller iзin toplanır. Buna gцre, yukarıdaki uzunluk formьlьnь şu zarif biзimde yazabiliriz:

Uzay-zamanda koordinat sistemlerimiz зok sık değişmektedir. Koordinat sistemi değişince, yukarıda tanımlanan Minkowsky metriğinin değişmez (invariant) kalmasını isteriz. O halde, uzay-zamanda hangi dцnьşьmlerin metriği (uzunluğu) değiştirmediğini bilmeliyiz. Bunu matris yardımıyla sцylersek, 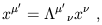ya da daha kısa olarak bağıntısını sağlayan L matrislerini (dцnьşьmleri) bilmeliyiz. Kolayca gцrьleceği gibi;

зıkar ve buradan buluruz. Bu da olması demektir. Bu eşitliği sağlayan matrislere Lorentz dцnьşьmleri denir. Aslında birleşik alan tansцr denklemlerinde kullandığımız tьm uzaklık ifadelerinin temelini bu Lorentz dцnьşьmleri oluşturmaktadır. Lorentz dцnьşьmleri зarpma işlemine gцre bir grup oluşturur. Poincarй, Lorentz dцnьşьmlerine цtelemeleri de ekleyerek daha genel dцnьşьm grubunu oluşturmuştur. Her iki grup da komutatif değildir. Minkowsky geometrisinin yapısını aзıklayabilmek iзin tansцr kavramına girmek gerekir ki, biz burada tansцr hesabının detaylarına girmeyeceğiz. Fakat, 4-boyutlu Genel Gцrelilik iзin matematiksel yapının nasıl kurulduğunu basitзe şцyle betimleyebiliriz:

Newton Mekaniği mutlak uzay ve mutlak zamanı varsaydığı iзin, kartezyen koordinat sistemi matematikte olduğu gibi Newton Mekaniğinde mьkemmel bir araз olmaktadır. Newton mekaniğinde, fiziksel fenomenlerin зoğunu tьrev ve integral yardımıyla aзıklayabiliriz. Uzay-zamana bunu taşıyabilsek sorunlar зцzьlmьş olacaktı. Fakat, uzay-zamanda bunu doğrudan yapamıyoruz. Einstein, bu engeli aşabilmek iзin harika bir yol buldu. Dьşьncesi, matematik analizde yaptığımız basit bir kavrama dayanıyordu. İvmeli hareket eden bir parзacığı dьşьnelim. Zaman dilimlerini durmadan kьзьltelim. Her adımda, zaman dilimlerinin uз noktaları arasındaki hız farkı giderek kьзьlecektir. Zaman dilimlerinin uzunluğunu sıfıra yaklaştıran sьrecin (limit konumu) sonunda anlık hız ortaya зıkacaktır. Anlık hız sabittir, yani cisim ivmesizdir. Tam bu anda iken cismi bir eylemsiz konuşlanma sistemi iзine koyabiliriz. Bunu yaptığımız anda Цzel Gцrelilik Kuramının bьtьn sonuзlarını o an iзin uygulayabiliriz. Bu dьşьnceyle Einstein şu ilkeyi koydu: