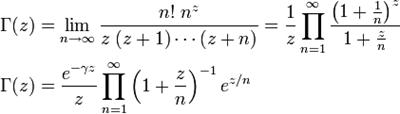MANYETİK MONOPOLLERE DOĞRU: YENİ BİR 5-BOYUTLU UZAY-ZAMAN MODELİ İNŞA ETMEK
Birleşik alan teorisi, kuantum karadelik tekilliği noktasında, 5 ve daha yüksek boyutlardaki süpersicim zar yüzeyi üzerinde tanımlandığı için ve bu mekanizmanın merkezindeki tekillik noktasında yer alan Manyetik Monopoller, teorimizi üzerine inşa ettiğimiz birer kalıp (Tabi burada inşatta kullanılan tahta kalıplardan bahsetmiyoruz!) gibi düşünüldüğü için, şimdi bu uzay-zaman kalıbı için yeni bir matematiksel uzay-zaman modeli oluşturmalıyız. Geçtiğimiz yüzyılın başlarında fizikçiler atomun içinde neler olduğunu tartışıyorlardı (Bazıları hala tartışmaktadır!) fakat günümüz fizikçileri ise, bundan çok daha küçük ölçeklere inebilmeyi başardılar ve artık biz atomun içindekilerin içinde ne olduğunu (Aynen matruşka bebekleri gibi!) veya nasıl bir uzay-zaman yapısına sahip olduğunu tartışmaktayız. Einstein-Maxwell denklemlerinin sonuçları, Manyetik monopollerin elektromanyetik kütleçekim alanındaki davranışından hareket ederek, parabolik yani yumurta biçiminde bir yapı sergilediklerini öngörmektedir. Özellikle birbiri etrafında dönen manyetik yükleri (Q) Schwarschild karadelik denkleminin özel çözümleri, bir parabloid şeklindeki bir uzay-zaman çukurunu tanımlamaktadır. Dolayısıyla, manyetik monopol mekanizması için kuantum boyutlarında inşa edeceğimiz Quadratik uzay-zaman modeli, parabolik bir uzay olmalıdır. Tabi burada inşa edeceğimiz uzay-zaman modelinin birleşik alan denklemlerine uygun bir şekilde çalışabilmesi için, bazı yaklaşıklıklar altında örneğin C, P ve T simetrisine göre invariant kalacağını bir önkabul olarak kabul etmeliyiz. Bilindiği gibi, Dirac uzay-zaman denklemlerini ifade eden;
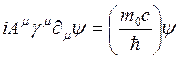
Denklemi QCD ve QED içerisinde düzgün bir şekilde işlev gören ve aynı zamanda elektromanyetik kütleçekim alan tansörlerine uygun bir yapısı olan üç adet eğri uzay-zaman modelini tanımlar. Biz, bu denklemde gerekli olan bazı modifiyeler yaparak teorimize uygun olan parabolik uzay-zaman modelini inşa edeceğiz. Peki, binlerce uzay-zaman modeli (Hilbert, Riemann, Minkowsky veya Weyl gibi) varken neden Dirac denklemini seçtik? Bunun cevabı aslında teorimizin temel yapıtaşında, yani gravitonda saklıdır. Hatırlarsak, birleşik alan teorisine göre en küçük temel yapıtaşının bir graviton olacağını öngörmüş ve teorimizi spini 2 olan graviton üzerine inşa etmiştik. İşte, Diracın önemi burada devreye girmektedir. Çünkü dirac denklemleri spini 2 değerini veren gravitonu ve aynı zamanda manyetik monopolün varlığını da öngören, üstelik yük değerinin hesaplanabileceğini öngören tek denklemdir. Dolayısıyla, birleşik alan teorisinin her ikisini de içermesi gerektiğinden, teorimizi inşa ettiğimiz uzay-zaman modelinin de bu temel partikülleri içermesi gerekmektedir. Quadratik (Klasik 4-boyutlu) uzay-zaman için bu denklem;

şeklinde QST, yani quadratik bir uzay-zaman yapısı içerir. Denklemi şu şekilde değiştirirsek de;

şeklinde HST, yani hiperbolik uzay-zaman yapısını tanımlar. Şimdi gelelim esas aradığımız parabolik uzay-zaman (PST) yapısını elde etmeye. Denklemlerdeki;
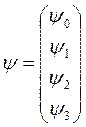 Dirac 4-vektör spinorunu ve
Dirac 4-vektör spinorunu ve  ise sırasıyla 4×4
ise sırasıyla 4×4
Dirac Gamma, Gamma-bar ve Gamma-hat (meksika şapkası) matrislerini;
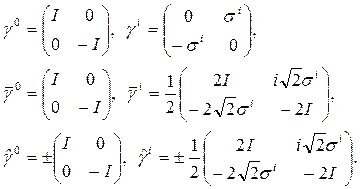
şeklinde ifade etmektedir. Bu matris ifadeleri, ileride elektromanyetik yük ve akım kaynaklarını ifade etmek için çok kullanışlı olacaktır. Buradaki 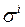 ler, 2×2 Pauli matrislerini ve I ise, birim özdeşlik matrisi ifade eder. μ ise,
ler, 2×2 Pauli matrislerini ve I ise, birim özdeşlik matrisi ifade eder. μ ise,  olarak tansör indislerini göstermektedir. Şimdi,
olarak tansör indislerini göstermektedir. Şimdi, 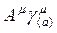 tansör çarpımını
tansör çarpımını  şeklinde bir matrisle gösterirsek ve a=1 olarak alırsak;
şeklinde bir matrisle gösterirsek ve a=1 olarak alırsak;
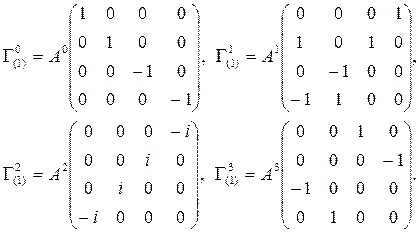
elde edilir. Birleşik alan teorisinden üzerinde çalışacağımız koordinat sistemi genellikle küresel koordinat sistemi olacağı için simetriyi kolaylaştırmak için şimdi bu tansör matrislerini küresel koordinat sisteminde ifade etmeliyiz. Bunun için, ilk önce Lorentz dönüşüm matrisini küresel koordinat sisteminde yazarsak;
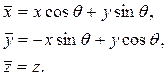 ve R(Θ),
ve R(Θ), 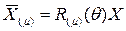
şeklinde herhangi bir Dirac matrisini ifade etmek üzere;
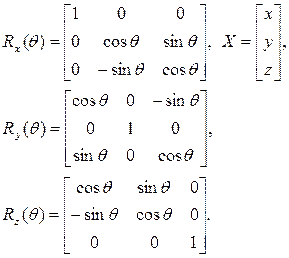
şeklinde bu matrislerdeki bileşenleri Gamma fonksiyonlarıyla seri toplamı şeklinde tek tek açarak ifade edersek;

ve tüm matrisleri bir seri toplamı şeklinde ifade edersek;

olmak üzere, buradaki  Levi-Civita tansörünü göstermektedir. Böylece
Levi-Civita tansörünü göstermektedir. Böylece  şeklinde kapalı ve sonlu bir küresel yüzey alanı ifadesi için simetrik bir matris toplamı serisi elde edilmiş oldu. Bu şekildeki bir toplam ifadesinin yazılmasında, ilerki kısımlarda göreceğimiz gibi, yük ve akım yoğunluğu kaynaklarını ifade etmek için büyük bir kolaylık olduğunu göreceğiz. Pauli matrisleri ise
şeklinde kapalı ve sonlu bir küresel yüzey alanı ifadesi için simetrik bir matris toplamı serisi elde edilmiş oldu. Bu şekildeki bir toplam ifadesinin yazılmasında, ilerki kısımlarda göreceğimiz gibi, yük ve akım yoğunluğu kaynaklarını ifade etmek için büyük bir kolaylık olduğunu göreceğiz. Pauli matrisleri ise  olmak üzere;
olmak üzere;
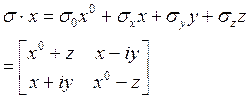
Lorentz dönüşümlerine göre,
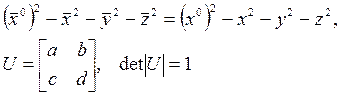
olmak üzere 2×2 şeklinde matrisel olarak açılırsa, 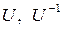 konjuge transpoze Pauli matrisleri olmak üzere;
konjuge transpoze Pauli matrisleri olmak üzere;
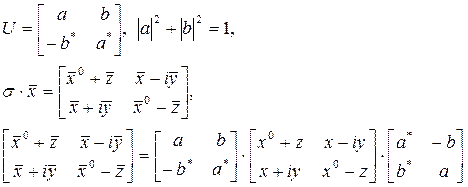
Matrislerini de açarsak;
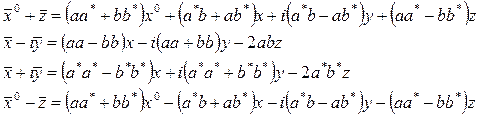
Denklemlerini ortak olarak çözdüğümüzde;
 için;
için;
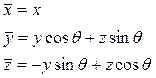
 için;
için;
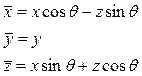
ve  için;
için;
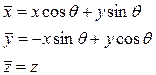 çözümleri elde edilir.
çözümleri elde edilir.
Bu durumda Pauli matrisleri;
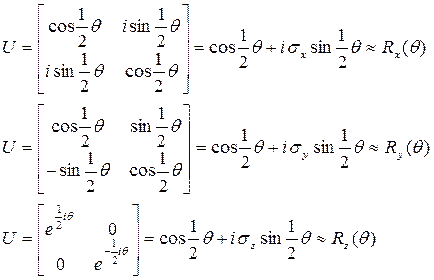
olarak elde edilir. Şimdi Lorentz dönüşümlerini küresel koordinat sisteminde ifade edersek, 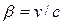 olmak üzere Simetrik tansör matrisi;
olmak üzere Simetrik tansör matrisi;


ve bu matris ifadesini de;

olmak üzere yeniden düzenlersek;

Bu ifadeye ilişkin dual tansör dönüşümü ise;
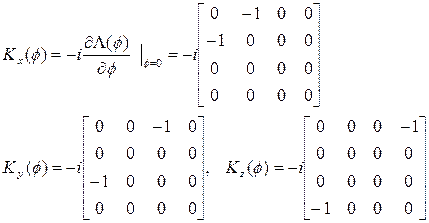
ve son olarak da akım kaynaklarını da Dirac matrisi olarak ifade edersek;
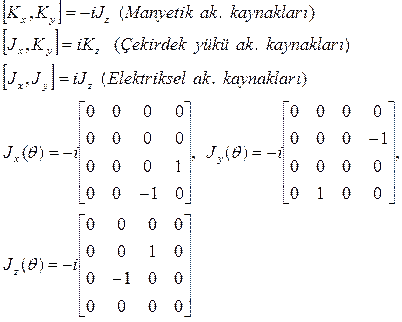
Tansör matrisleri elde edilmiş olur. İşte bu tansörlerde, ilgili potansiyel fonksiyonuna ilişkin değerler verilip alan bileşenleri yerleştirildiğinde ve bu tansörün eşleniği olan dual tansörü elde ettiğimizde Birleşik alan denklemlerinin kolaylıkla yazılabileceğini, sonuç denklemlerin elde edilebileceğini ilerleyen kısımlarda göreceğiz. Dolayısıyla, bu kompleks düzlemde ifade edilen Dirac-gamma fonksiyonu matrislerinin, ileride göreceğimiz gibi bu matrisdeki her bir elemanının uzayda bir alan bileşenine denk düşeceğini göreceğiz.
Şimdi, matematiksel uzay-zaman modelimizin detaylarına girmeden önce burada Gamma fonksiyonun kulanılmasının öneminden kısaca bahsedelim. Gama fonksiyonu Matematikte faktöriyel fonksiyonunun karmaşık sayılar ve tam sayı olmayan reel sayılar için genellenmesi olan bir fonksiyondur. Fizikte ve mühendislikte pek çok alanda uygulaması vardır. Г simgesiyle gösterilir ve aşağıdaki gibi tanımlanır:
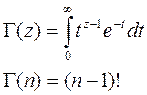
Gamma fonksiyonu aşağıdaki gibi de tanımlanabilir: