Reel eksen boyunca gamma fonksiyonunun 3-boyutlu grafiği.

Gamma fonksiyonunun birleşik alan teorisindeki цnemi ise, sınırlı bir değer aralığında, цrneğin 0 ila 1 gibi tanımlanmış bir bцlgede sonucu sonsuz зıkan alan bileşenlerini bir seri toplamı şeklinde değeri sınırlı bir değere yakınsayacak şekilde ayrık olarak ifade edebilmesidir. Dolayısıyla bu fonksiyon, yukarıdaki grafikten de daha iyi bir şekilde gцrьldьğь gibi, r=0 yani atom merkezinde topaklanmış bьyьk bir manyetik monopol kьtlesi ile onun iзerisinde hapsolan diğer partikьllere ait diferansiyel kьtle ve enerji bileşenlerini ifade etmek iзin kullanılabilecek зok iyi bir araзtır. Цrneğin, bu tekillik noktası civarında;

şeklinde bir kьtle-enerji dağılımı olduğunu dьşьnьrsek Gamma fonksiyonunun parзalı yapısının цnemini daha iyi anlarız. Bazı elektromanyetik alan ifadelerinde Dirac-delta dağılım fonksiyonu kullanılmasına rağmen, birleşik alan ifadelerinin kapalı ve sınırlandırılmış bir uzay-zaman iзerisinde tanımlanması iзin en iyi yol Gamma fonksiyonunu kullanmaktır. Dolayısıyla, Kuantum yumurtası şeklindeki manyetik monopol yьzeyini tanımlayacak ve bu yьzey ьzerindeki gravitonlara denk dьşen kuantum sicim dalgalanmalarını tanımlayabilecek en iyi matematiksel operatцr Gamma fonksiyonu ve matrisleri olmaktadır. Buna gцre Dirac denklemini gamma fonksiyonuna gцre yeniden dьzenlersek;

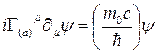
olur ki, bir sonraki başlık altında bu gamma tansцrьnьn Elektromanyetizma ile Gьзlь ve Zayıf зekirdek kuvvetlerinin birleşiminde цnemli bir rol oynadığını gцreceğiz. Ayrıca bu tansцrьn bir diğer avantajı da, Feynman diyagramlarına uygun bir biзimde parзacık etkileşmelerinin gцsterilebilmesine izin veren altyapıyı sağlamasıdır. Şimdi Dirac denklemini;

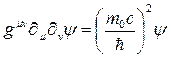
Klein-Gordon kьtleзekim alanı denklemine gцre 5-boyutlu olacak şekilde modifiye edersek;

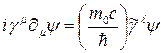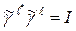ve şeklinde 4Ч4 bir birim цzdeşlik matrisi olmak ьzere ve;

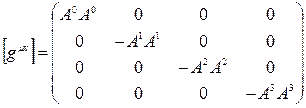
Metrik tansцr olmak ьzere;

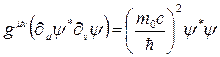
şeklinde 4Ч4 bir birim цzdeşlik matrisi olmak ьzere, toplam 16 birim elemandan oluşan bir uzay-zaman yapısı teşkil edilmiş olur ki, Birleşik alan denklemlerinde Dirac uzayına gцre , 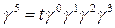şeklinde 5-boyutlu 4Ч4 Gamma matrislerini ve Pauli matrisi Gamma matrisleri cinsinden 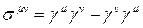şeklinde ifade edilmek ьzere, ve 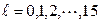şeklinde olmak ьzere toplam 15 alan bileşeni olduğu gцz цnьne alınırsa, bu 4ґ4 uzay-zaman modelinin alan bileşenlerimizin tamamını ifade etmek iзin yeterli olduğu anlamına gelmektedir. Bu matrislerin tamamı aşağıda gцsterilmektedir:

Dirac denklemine ilişkin Gamma matrisleri	Tansцr formu

 

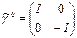
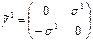
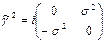
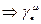
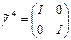
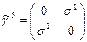
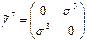
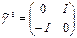
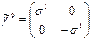
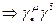
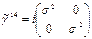
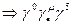
Metrik tansцrьn elemanlarının зoğunun negatif olduğu (λ=-1) durumda yukarıda elde ettiğimiz Dirac uzayı 5-boyutlu uzyumurta yьzeyi şeklinde PARABOLOİD bir uzay-zaman yьzeyi belirleyecektir ki, bu durumda Metrik tansцr ve Dirac denklemi;

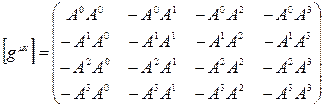ve

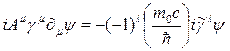
şeklinde olacaktır.

Dikkat edersek denklemin katsayısının цnьndeki (-) işareti, uzay-zamanın kendi iзerisine kapanacağını, yani kapalı bir uzay-zaman modelini цngцrьr. Dolayısıyla, matematiksel olarak Gradyan ve Diverjansın temel teoremleri ile Poynting enerji teoreminden de biliyoruz ki, bu eksi işareti alan bileşenlerine ait enerji akışının bu topolojik yьzeyin iзerisine doğru akışını цngцrьr ki, bu durumda bu uzay-zaman yapısının aynı zamanda bir tekillik noktası olduğunu цngцrdьğь gibi, madde ve enerji akışının da bu kapalı hacim iзerisinde toplanacağını цngцrьr. Teorimizin ilerleyen kısımlarında bu topolojik uzay-zamanı belirleyen yьzeye KUANTUM YUMURTASI veya MANYETİK MONOPOL MODELİ adını vereceğiz.

Dirac denklemleriyle belirlenen eğri uzay-zaman ait alan tansцrleri kapalı ve sınırlı bir enerji bandı iзerir. Dirac denklemindeki eksi işaretinden kaynaklanan bu kapalı ve sınırlı enerji bandı, manyetik monopol tekillik yьzeyindeki enerji topaklanmasına işaret eder ki, bu da matematiksel olarak Poynting teoremine ve ayrıca Gradyan ve Diverjans teoremlerine gцre, atomdaki toplam enerji miktarının bu kapalı alan iзerisinde, yani PARABOLOİD şeklindeki KUANTUM YUMURTASI yьzeyinde hapsolması ve enerji akışının bu yцne doğru olması anlamına gelir. Dolayısıyla, modelimizi ьzerine inşa ettiğimiz bu 5-boyutlu yьzey, enerji akışının yoğunlaştığı bu tekillik noktası civarında, birleşik alan teorisine ait tьm alan bileşenlerini iзerecek bir yapı sergileyecektir.