GENEL DURUMDA 5-BOYUTLU İNDİRGENMİŞ ”ELEKTROZAYIF ALAN TANSЦRЬNЬN” ELDE EDİLMESİ VE SONUЗLARI

Şimdi, tekrar tansцr hesabına dцnelim. Euler-Lagrange denklemi:

olmak ьzere; Einstein-Yang-Mills alan denklemleri;

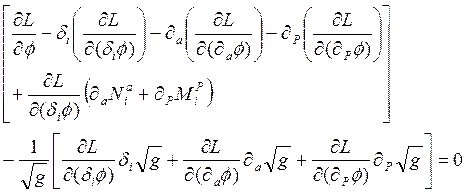
D’alembert operatцrь cinsinden Einstein-Yang-Mills alan tansцrь;

(□- M²) A_μv

ve Lagrange operatцrь cinsinden Elektromanyetik alan tansцrь;

şeklinde olmak ьzere, burada 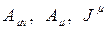sırasıyla antisimetrik tansцr ile antisimetrik tansцre ilişkin yьk ve akım kaynaklarını iзeren 4-vektцr bileşenleri ile 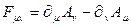şeklinde elektromanyetik alan bileşenini gцstermektedir. f ve ζ ise, extra koordanatlara bağlı (5 ve ьzeri) katsayı fonksiyonlarını; φ ve ise, extra koordinatlara bağlı skaler vektцr bozonlarına ait skaler potansiyel fonksiyonlarını ifade etmektedir. Einstein alan denklemlerini vektцr bozonlarının kьtlelerini de iзerecek şekilde yeniden Lagrange denklemine gцre ifade edersek;

(□- m_φ²) φ^(ph)

olur. Burada, m_φ ve m_ψ vektцr bozonlarının kьtlesini gцstermektedir. Bu iki denklemi birlikte зцzьp, m²’li terimleri tek bir kьtle altında ifade edersek;

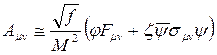
denklemi elde edilir. Bu denklem, elektrozayıf alanına ait antisimetrik tansцrь belirlediğinden ve diyagonal eksene bağlı quadratik bileşenlerin tamamı sıfır olması gerektiğinden, toplam diferansiyel akım yoğunluğu ifadesi;

olmak ьzere, зekirdek hacmi iзerisindeki toplam yьk simetriden dolayı sıfır olması gerektiğinden;

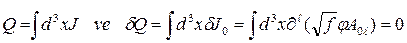olarak bulunur. Şimdi antisimetrik elektrozayıf tansцrьnь, elektrik ve manyetik alan vektцrleri cinsinden ifade edersek;

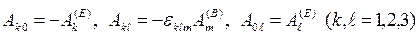
olur ve matris formunda ise;

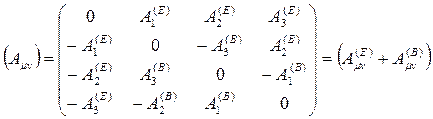
Dirac spin tansцrь ise, spinorları cinsinden;

olur. Bu durumda, başta verdiğimiz Einstein-Yang-Mills Lagrange genel denklemini yukarıdaki eşitliklere gцre yeniden yazarsak;

Bu durumda, elektrozayıf alan bileşenlerine ait D’alembert denklemlerinin yeni formu şu şekilde olur:

(□- M²)

(□- M²)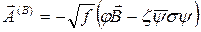

Bu son denklemlere dikkat edersek, simetrik oldukları ve manyetik monopollerden kaynaklanan, vektцr bozonu etkileşimlerinin denklemlerin sağ tarafında yer aldığı gцrьlьr. İşte bu kaynaklar, aslında biraz sonra gцreceğimiz gibi, burada ve ile gцsterilen W ve Z bozonları ile M kьtlesiyle gцsterilen ki, burada aslında M kьtlesi зok daha bьyьk bir kьtle iзeren Manyetik monopole işarettir, Higgs bozonlarına denk dьşecektir ve teknik olarak elektromanyetizma ile зekirdek kuvvetlerini temel dьzeyde birleştiren ara denklemler olduğu gцrьlecektir. Ayrıca, denkelemlerdeki simetriye dikkat edersek, bir цnceki başlıkta ele aldığımız kьtleзekimiyle elektromanyetizmanın birleşimini iзeren simetrik Maxwell denklemlerine ne kadar benzediği de şaşırtıcıdır. Yukarıda verilen D’alembert operatцrь altında tanımlanan ikinci dereceden Einstein-Yang-Mills alanında, M kьtlesine sahip olan Ф skaler alan fonksiyonuyla temsil edilen vektцr bozonlarını Klein-Gordon denklemiyle ifade edersek;

(□ + m²)

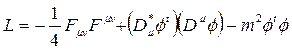
Ve bu denklemi de Proca denklemine uyarlarsak;

□

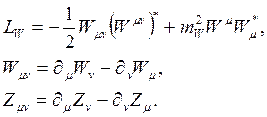
taşıyıcı vektцr ara bozonlarını belirleyen tansцr denklemlerini elde etmiş oluruz. Buradaki “*” işaret Hodge operatцrьnь ve “t” transpoze/ters (inverse) matris operatцrьnь gцstermektedir. Buna gцre, Bozonik elektrozayıf kurama ait Lagrange operat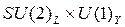цrь, Yang-Mills ayar dцnьşьmь altında;

şeklinde olacaktır. Buradaki “ ’ ” yцnlь tьrevi ve “Ф” skaler alan fonksiyonu, standart modeldeki, yьkleri kesirli veya tam sayı değeri veren partikьl зiftlerini gцstermektedir. Bu fonksiyonun iзerisinde pek зok partikьl tanımlı olarak yer alabilir ki, bunların iзerisinde şimdiye kadar teorik olarak цngцrьlen en ağır olanının Higgs bozonu olduğunu sцyleyebiliriz. Dolayısıyla, bu dьşьnce mantığı daha ağır kьtleli partikьllerin ortaya зıkmasının цnьnь aзmaktadır. Bu durumda, Ф skaler alan fonksiyonunu atomun merkezinde yoğunlaşan partikьl зiftlerine ait olanlarınkini φ⁰ ve tekillik merkezinin dışında kalan partikьl зiftlerine ait skaler alan bileşenlerini de φ⁺ ile gцstermek suretiyle; atomun tamamı iзin tanımlanan toplam skaler alanı, bu iki skaler alan bileşeninin vektцrel toplamından oluşacak şekilde vektцrel olarak gцsterirsek;

ve kovariant alan tansцrь bileşenlerini de;

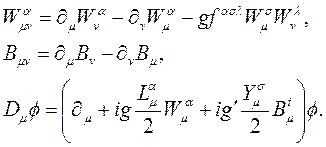
şeklinde tanımlarsak Elektrozayıf alana ilişkin temel tansцr denklemlerini elde etmiş oluruz. Burada manyetik alan bileşeninin, 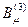şeklinde teorimiz iзin цzel bir цnemi vardır ki, ilerleyen kısımlarda bu bileşenin alan denklemlerinin yazıldığı 5-boyutlu uzay-zaman yapısına helezonik bir yapı kazandırdığını, dolayısıyla bu yapının da ilginз ve beklenmedik bir şekilde kьtleзekiminin helezonik mekanizmasını doğal olarak oluşturan bir mekanizmayı tetiklediğini gцreceğiz. Dolayısıyla, 4-boyutlu uzay-zaman iзin yazılan Einstein alan denklemlerinde bu bileşenin etkisi gцrьlmezken, 5-boyutlu uzay-zaman iзin yazılan Einstein-Schwarzschild kapalı alan denklemlerinin цzel tekillik зцzьmlerinde, kilit bir etkiye sahip olduğunu ve bu bileşenin etkisiyle uzay-zamanın dьz (lineer) bir eğrisel yapıdan helezonik (nonlineer) bir eğrisel yapıya doğru kaydığını gцreceğiz. Elektromanyetik alan bileşenleri ile Zayıf зekirdek kuvveti arasındaki etkileşimleri gцsteren tansцr eşitliklerini de yazacak olursak;

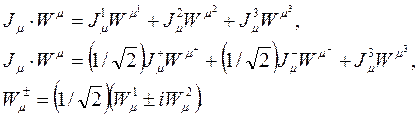
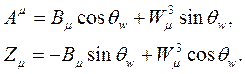
şeklinde Elektrozayıf kuramına ait temel tansцr denklemlerini ve partikьl зiftleri etkileşimlerini belirleyen denklemleri elde etmiş oluruz. Buradaki Θ aзıları zayıf etkileşim esnasındaki partikьller arası зarpışma aзılarını g ise gьзlь зekirdek kuvvetin taşıyıcı yьkь olan Gluonları gцstermektedir. Ayrıca, buradaki tansцr ifadelerine dikkat edersek, toplam altı adet bozon iзerdiği gцrьlьr ki, Ф skaler alan fonksiyonu ьз adet Goldstone bozonunu (Ф₁, Ф₂, Ф₃) tanımlarken ve W ve Z vektцr ara bozonları (W^-, W⁺, Z) bozonları arasındaki ilişki aşağıdaki gibidir:

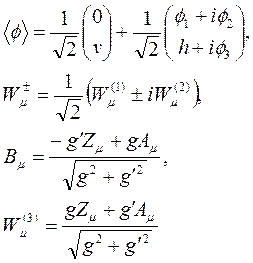
Burada ara işlemleri gцstermeden elektrozayıf etkileşimleri iзeren sonuз denklemleri yazarsak;

 

şeklinde olur. Burada, “h” ve “m_h” birleşik alan teorisine giden yoldaki цnemli bir kцşe taşı olan “Higgs” bozonuna; “ v ”, elektromanyetik alanın taşıyıcı bozonu olan fotonlara ve “g” gluonlara işaret etmektedir. Dikkat edersek, son denklemlerde partikьl etkileşimlerini belirleyen sonuз ifadelerinin parзalı bir seri toplamı şeklinde yazılabildiği gцrьlmektedir. Bu da bize, bu denklemlerde yer alan “η” ve“ζ”gibi ekstra (kapalı boyutlar boyunca) koordinat sistemlerine bağlı Higgs bozonundan daha ağır partikьl ve bozon зiftlerinin de var olabileceğini kanıtlamaktadır. İlerleyen kısımlarda, tekrar bu mekanizmanın yapısına ve Higgs bozonunun birleşik alan teorisindeki цnemine dцneceğiz..

Dolayısıyla, her ne kadar bu зalışmamızda ele aldığımız birleştirme teorimiz, kainattaki en ağır partikьllerin planck цlзeğinde yer alan manyetik monopoller ağı ьzerine inşa edilmiş graviton цrgьsь olarak kabul etse de; elde ettiğimiz bu sonuз denklemler, atomaltı dьnyada daha pek зok bilinmeyen partikьlьn ve vektцr ara bozonunun varlığına işaret etmektedir. Şimdi gelelim bu sonuз denklemler altında, Elektrozayıf kuvvete ait tansцr matrisi denklemlerini, yani birleşik alan teorisinde kullanacağımız esas denklemleri oluşturmaya.

Bilindiği gibi, 4-Vektцrlerin Lorentz dцnьşьmьnь hatırlarsak:

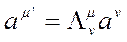
olup, burada Λ Lorentz dцnьşьm matrisi aşağıdaki gibidir:

olur. ise, μ. satır v. sьtun elemanıdır. İkinci dereceden (yani iki indisli) bir tansцr dцnьşьrken, her bir indis iзin birer gerekir:

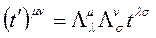
Dцrt boyutta ikinci dereceden tansцrьn 4Ч4=16 elemanı vardır;

Fakat, 16 elemanın her biri farklı olmayabilir. Цrneğin, Simetrik Tansцr:

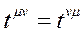(Simetrik Tansцr)

olarak tanımlanır. Bu durumda kцşegene gцre simetrik elemanlar eşit olur;

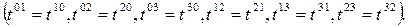
6 eleman tekrarlandığı iзin tansцrьn 10 farklı elemanı olabilir. Benzer şekilde, Antisimetrik Tansцr:

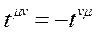(Antisimetrik Tansцr)

olarak tanımlanırsa, bunun 6 farklı elemanı olabilir; daha цnceki 6 eleman eksi işaretli olarak tekrarlanır ve kцşegen ьzerindeki dцrt eleman sıfırdır. Buna gцre, en genel antisimetrik tansцr şцyle olur:

Şimdi, dцnьşьm kuralının antisimetrik tansцrь nasıl dцnьştьrdьğьne bakarsak;

Fakat, λ = 0,1 dışında olacaktır. Benzer şekilde σ = 0,1 dışında olur. O halde, зift toplamadan dцrt terim gelir:

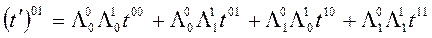
Antisimetrik Tans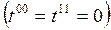цr iзin, ve olduğunu gцz цnьne alırsak;

olarak bulunur. Diğer elemanlar iзin de benzer dцnьşьm hesabı yapılırsa;

Bu ifadeler ise, elektromanyetik alan tansцrь ile aynı yapıdadır. Bu durumda karşılıklı elemanlara bakarak 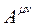antisimetrik elektrozayıf alan tansцrь elemanlarını şцyle kurabiliriz. , elektromanyetik alan tansцrьnь; zayıf зekirdek kuvveti alan tansцrьnь ve de gьзlь зekirdek kuvvetine ait alan tansцrьnь gцstermek ьzere;

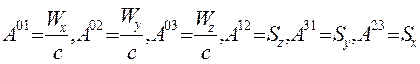
Alan tansцrьnь matris şeklinde gцsterirsek:

 

Bu tansцre ilişkin, 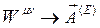, , ve 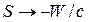değişimleri yapılarak ve zayıf ve gьзlь зekirdek kuvvetlerinin sicim dьzeyinde kendi aralarında dцnьşьmlь olduğunu varsaydığımızda oluşturulan “Dual Tansцr” ise;

olur.

Lorentz dцnьşьmьnden yararlanarak yьk ve akım yoğunluklarını tanımlarsak:

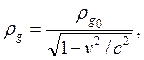
Burada 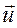akım yцnьndeki birim vektцr, ρ₀ ele alınan referans sistemine bağlı “Цz yьk yoğunluğu” ve c ışık hızı olmak ьzere; yьk ve akım yoğunluğu iзin bir 4-Vektцr oluşturursak; 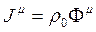ve Elektriksel renk yьkь ve Gluon (Kuark) akım yoğunluğu 4-vektцrьnьn bileşenleri de şцyle kurulmuş olur:

ve

Benzer şekilde ve

koyarak; Zayıf ve Gьзlь зekirdek kuvveti iзin yazılan, Bozonik Akım yoğunlukları iзin de bir 4-vektцr oluşturursak;

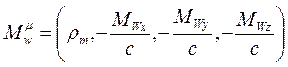
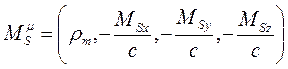
olur. Bu durumda elektrozayıf tansцr denklemlerinin tьmь şцyle цzetlenebilir:

,

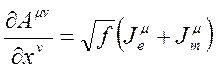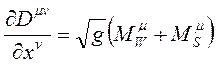
Buradaki f ve g Dirac-Gamma ayar dцnьşьm matrisleridir. Bu ifadeye ilişkin vektцrel formda elektromanyetik alan tansцrьyle bağlayıp, bozonik vektцr alanına ilişkin 4-Boyutlu toplam Antisimetrik Tansцr ifadesini yazarsak:

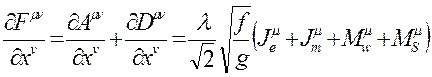
olur. Tansцr ifadesini matrisel vektцr alanı şeklinde gцsterirsek;

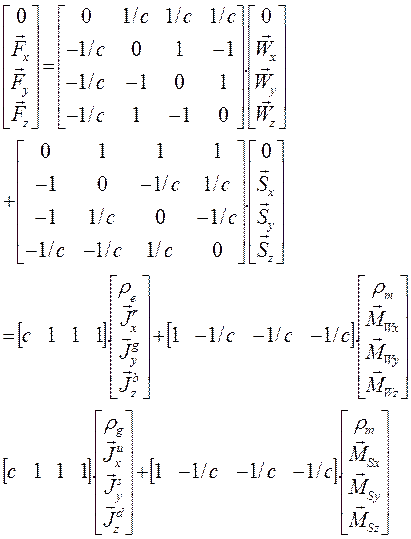
olarak yazılabilir. Bunun da matrisel formdaki 4Ч4 boyutlu simetrik alan bileşenleri cinsinden aзılımını yaparsak;

Genel formdaki Elektrozayıf alanına ilişkin Tansцr matrisleri elde edilmiş olur.

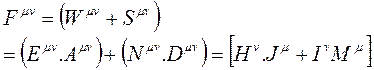
olarak yazılırsa, Matris ifadelerindeki tansцr katsayıları;

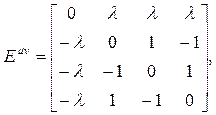
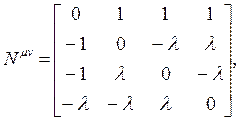
şeklinde olacaktır. Şimdi elektrozayıf kuramına ilişkin temel Maxwell alan denklemlerini de teşkil edersek, Elektromanyetizma ile зekirdek kuvvetlerinin bir ara birleşimini tanımlamış olacağız ve birleşik alan teorisine giden ilk adımımızı atmış olacağız.

Dikkat edersek, denklemlerde Elketromanyetizma, Gьзlь ve Zayıf зekirdek kuvvetlerinin birleşimini gцsteren Maxwell denklemleri gayet şık, basit ve simetrik bir şekilde tanımlanmıştır. Gerзekte, elbette ki bu bağlantı зok daha karmaşık denklemler iзermesi gerekirken, biz burada kuantum mekaniğinin ileride bahsedeceğimiz bir ilkesini ihlal ederek bu sonuca ulaştık ve bazı yaklaşımlar yaparak temel kuvvet alanların aynı yapıda birleşik bir ana kuvvetin parзaları gibi davrandığını gцstermeye зalıştık. Buradaki denklemlerde yer alan, c ışık hızı ve λ SU(2) daha цnce paraboloid uzay-zaman yapısına bağlı olarak değişen atomik hermitian simetrik Dirac-Gamma matris katsayılarıdır. Dikkat edersek, tьm denklemlerde elektromanyetizma ile zayıf зekirdek kuvvetinin mьkemmel bir bağlantı iзerisinde olduğu gцrьlmektedir ki, bu da bize bu ikisinin aslında tek bir ana kuvvetin iki parзası gibi davrandığını isbatlamaktadır. Burada m_h higgs bozonunu m_W ile m_W ve m_Z, vektцr ara bozonları gцsterilmektedir. Gerзi, denklemlerde sadece W bozonu yer almakla birlikte, tansцr bileşenleri iзerisinde Z bozonunun da bu matris iзerisinde birleşik olarak temsil edildiğini dьşьnebiliriz. Ayrıca, kuantum dьzeyinde birleştirme işlevini gerзekleştiren gьзlь зekirdek kuvvetiyle bağlantılı olan temel partikьllerin W ve Z bozonları ile birlikte renkli elektrik yьkleri () ve gluonların () ve dolayısıyla gьзlь зekirdek kuvvetinin de dahil edilmesiyle manyetonları (manyetik monopolleri) da iзerisine aldığı gцrьlmektedir. Dolayısıyla, bu kısımda ele alınan birleştirme işlemi, elektromanyetizma ile зekirdek kuvvetlerini tam bir basitlik iзerisinde, gayet estetik ve simetrik birleşimini sunmaktadır. Peki, kuarklar nereye gitti? Tansцr denklemlerine dikkat edersek, kuarkların gluonların iзerisinde yer aldığı gцrьlmektedir. Buna, зekirdek fiziğinde Kuark-Gluon plazması adı verilir ki, QCD’de bu kavram da aslında burada gцsterildiği gibi, ikisinin sicim boyutlarında dьşьnьldьğьnde evrenin ilk anlarında tek bir yapının iki ayrı birleşimi olabileceğini ifade eder. Dikkat edersek, son terimde Higgs bozonunun belirlemek iзin gerekli ayar alanının yaklaşık v=246 GeV olduğu belirlenir. Buradan da anlaşılıyor ki, diğer bozonlarla Higgs bozonu kuvvetli bir şekilde etkileşmektedir ve bu etkileşmenin ortaya зıkması iзin ise yaklaşık 200 GeV’luk bir eşik enerjisine gelinmesi gerektiği anlaşılmaktadır (Bkz: Aşağıdaki eşik enerjisi grafiği). Ortaya зıkan (y) ve (b) kuarkları ise;

şeklinde gцsterilenbilir. Burada b (blue) kuarkının kьtlesi, ve gцrece зok daha ağır olan t (top) kuarkının kьtlesi ve diğerleri de benzer şekilde olacaktır. Ayrıca bu denkleme gцre, SU(2) ayar dцnьşьmь altında şeklinde yьk toplamı sıfır olacağı iзin, elektrozayıf etkileşim tьm ayar grupları 5D»4D dцn. altında invariant kalacaktır.

 

Şimdi, elektromanyetizmayla zayıf nьkleer kuvvetin nasıl bir etkileşim yapısı oluğunu ve elektrozayıf kuramını biraz daha detaylı olarak inceleyelim. Bildiğimiz gibi, zayıf etkileşim birbirinden ayrıymış gibi duran QED, elektrodinamik kuramı ile QCD, gьзlь зekirdek kuvveti kuramını birleştirmektedir. Зekirdek iзerisindeki renkli yьk ve kuark akımları bir elektrik alan indьkleyecek ve bu alan da manyetik monopollerin oluşturduğu manyetik alanla birleşerek elektrozayıf sicim dalgalanmalarını oluşturacaktır. Klasik QED ve QCD mantığı iзerisinde, bu sicim dalgalanmalarının atom зekirdeği iзerisinde dьzgьn olarak dağıldığı varsayılabilir. Bununla birlikte, alanın kьtle yoğunluğu ve yьk miktarının fazla olduğu bцlgelerde yoğunlaşabileceği de dьşьnьlebilir. İlginзtir ki, elektromanyetizma ve gьзlь nьkleer kuvveti taşıyan kuvvet partikьlleri зok kьзьk kьtlelere sahip olmalarına rağmen, elektrozayıf kuramının taşıyıcı partikьlь olan W^± ve Z bozonları oldukзa ağır olması bu gцrьşь daha зok kuvvetlendirmektedir. Bu da bizi, tьmdengelimli bir dьşьnce tarzıyla, alan bileşenlerinin merkezi bir noktada, atom зekirdeğinin merkezindeki manyetik monopol kьtlesi civarında yoğunlaştığı fikrine gцtьrmektedir.

Цrneğin,civarındadır. Aslında, zayıf etkileşimin ana fikri Higgs mekanizmasına, Higgs mekanizması ise standart modele dayanmaktadır. Fakat, buradaki esas problem ise, Higgs parзacığının beklenenden зok daha ağır olması veya цmrьnьn зok kısa olmasındadır.